Элементарная теория металлоискателя
Для правильного, соответствующего поставленной задаче выбора рабочей частоты металлоискателя, размеров катушки, для определения предельных возможностей прибора данной чувствительности, для оценки влияния грунта и других мешающих факторов на поиск, необходимо получить соотношения, описывающие работу металлоискателя.
Для определённости будем анализировать металлоискатель индукционного типа с простой однообмоточной катушкой (моно-катушкой). Однако, полученные результаты будут полностью справедливы и для металлоискателей на основе измерения частоты, а многие выводы применимы и для приборов других типов. По возможности будем избегать привлечения сложной математики и неочевидных расчётных формул из справочной литературы, предпочитая более грубую оценку, но получаемую более простыми методами. Тем более, в большинстве случаев для решения практических задач высокая точность вычислений не требуется, часто достаточно лишь оценить порядок величин.
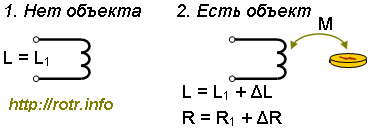
Рис. %img:dl
Принцип действия индукционного металлоискателя основан на влиянии проводящего ток предмета на расположенную поблизости катушку; при приближении предмета к катушке, изменяется её эквивалентная индуктивность и активное сопротивление (рис. %img:dl). Наша первоочередная задача состоит в вычислении этих изменений.
Влияние предмета на катушку объясняется тем, что проводящий предмет, который обладает собственной индуктивностью и активным сопротивлением, имеет магнитную связь с катушкой (пусть и слабую). Эта связь характеризуется взаимной индуктивностью, которая зависит от формы и размеров катушки, объекта и их взаимного расположения. При этом объект можно рассматривать как индуктивный элемент, замкнутый на своё активное сопротивление.
Соотношения, описывающие подобную систему хорошо известны из теории цепей, где они рассматриваются в разделе, посвящённом рассмотрению индуктивностей и взаимных индуктивностей. Этот же вопрос рассматривается в теории трансформаторов (систему катушка - предмет можно рассматривать как крайне несовершенный трансформатор с короткозамкнутым витком). Но, для полноты изложения, выполним вывод уравнений и здесь.
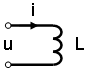
Рис. %img:eq_l
Напряжение u на индуктивности L и ток через неё i (рис. %img:eq_l) связаны следующим соотношением
$$
u=L \frac {di} {dt}.
$$
Здесь и далее мы предполагаем, что все рассматриваемые элементы являются линейными, что с высокой степенью точности соответствует действительности, поскольку в поле катушек отсутствуют материалы с нелинейными свойствами (считаем, что поблизости нет ферромагнетиков, а если и есть, то далеки от насыщения).
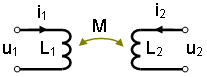
Рис. %img:eq_2l
При наличии магнитной связи с другой индуктивностью (рис. %img:eq_2l), напряжение на каждой индуктивности зависит не только от тока через неё, но и от тока через вторую индуктивность.
$$
\begin{equation}
\begin{cases}
u_1=L_1 \frac {di_1} {dt} + M \frac {di_2} {dt}, \\
u_2=M \frac {di_1} {dt} + L_2 \frac {di_2} {dt},
\end{cases}
\label{pm_eq}
\end{equation}
$$
в нашем случае L1 - индуктивность катушки металлоискателя; L2 - собственная индуктивность объекта, находящегося поблизости от катушки и тем самым влияющего на неё; M - взаимная индуктивность катушки и объекта. Мы сразу записали уравнения с учётом того известного факта, что M12 = M21 - взаимная индуктивность второй индуктивности по отношению к первой равна взаимной индуктивности первой индуктивности по отношению ко второй.
Здесь и далее, для величин, относящихся к катушке металлоискателя, будем использовать индексы 1, а для величин, относящихся к объекту поиска - индексы 2.
Рассмотрим случай синусоидального сигнала в катушке, при этом магнитные поля, токи в объекте, напряжения на индуктивностях будут также изменяться по синусоидальному закону с той же частотой. Поэтому имеет смысл воспользоваться методом комплексных амплитуд, благодаря чему дифференциальные уравнения \eqref{pm_eq} примут вид алгебраических, при этом оператор дифференцирования по времени заменяется умножением на коэффициент \(j \omega,\) где \(j=\sqrt{-1}; \ \omega=2\pi f\) - циклическая частота (f - частота сигнала):
$$
\begin{equation}
\begin{cases}
\dot U_1=j \omega L_1 \dot I_1 + j \omega M \dot I_2, \\
\dot U_2=j \omega M \dot I_1 + j \omega L_2 \dot I_2,
\end{cases}
\label{jm_eq}
\end{equation}
$$
До сих пор мы не учитывали собственные активные сопротивления катушки и объекта, они могут быть введены в рассмотрение как самостоятельные сопротивления, подключённые последовательно с индуктивностями; напряжение на катушке будет тогда определяться как сумма напряжения на индуктивности и напряжения на активном сопротивлении.
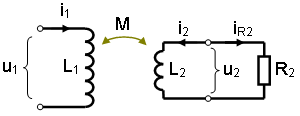
Рис. %img:eq_2lr
Активное сопротивление катушки металлоискателя включать в уравнения не будем, отнесём его к внутреннему сопротивлению источника сигнала. Активное сопротивление объекта R2 является нагрузкой для индуктивности объекта L2 (рис. %img:eq_2lr).
С помощью уравнений системы \eqref{jm_eq} выразим \(\dot U_1\) через \(\dot I_1\), тогда сможем вычислить комплексное сопротивление катушки как \(\dot Z_1=\dot U_1 / \dot I_1\) (при наличии рядом с катушкой влияющего предмета) и, сравнив с начальным \(\dot Z_{10}=j\omega L_1\), определить вносимое реактивное и активное сопротивление.
Воспользуемся тем, что \(\dot U_2=\dot I_{R2} R_2 =-\dot I_2 R_2\); положительные направления токов для двух связанных индуктивностей выбраны, как это принято для четырёхполюсников, чтобы уравнения для напряжений на индуктивностях имели вид \eqref{jm_eq}. Подставляем выражение для U2 во второе уравнение системы \eqref{jm_eq}, получаем
$$
-\dot I_2 R_2=j\omega M \dot I_1+j\omega L_2 \dot I_2,
$$
откуда выражаем
$$
\dot I_2=-\frac {j\omega M \dot I_1} {R_2+j\omega L_2}.
$$
Подставляя полученное для тока \(\dot I_2\) выражение в первое уравнение системы \eqref{jm_eq}, сможем выразить \(\dot U_1\) через \(\dot I_1\):
$$
\dot U_1=\dot I_1 \left(j\omega L_1+\frac {\omega^2 M^2} {R_2+j\omega L_2}\right),
$$
значит,
$$
\dot Z_1=\dot U_1 / \dot I_1=
j\omega L_1+\frac {\omega^2 M^2} {R_2+j\omega L_2}=
j\omega L_1+\frac {\omega^2 M^2(R_2-j\omega L_2)} {R_2^2+\omega^2 L_2^2}, \\
\dot Z_1=j\omega \left(L_1 - \frac {\omega^2 M^2 L_2} {R_2^2+\omega^2 L_2^2} \right)+\frac {\omega^2 M^2 R_2} {R_2^2+\omega^2 L_2^2}.
$$
Сравнивая полученный результат с начальным комплексным сопротивлением катушки \(j\omega L_1\), видим, что влияние находящегося рядом предмета проявляется в уменьшении индуктивности катушки и увеличении активного сопротивления. Индуктивность катушки изменяется на
$$
\begin{equation}
\Delta L_1=-\frac {\omega^2 M^2 L_2} {R_2^2+\omega^2 L_2^2}.
\label{delta_l1}
\end{equation}
$$
Трудность обнаружения предмета определяется не самим изменением индуктивности катушки, а относительным изменением (обычно минимальное фиксируемое относительное изменение индуктивности катушки является постоянной прибора). Поэтому запишем выражение и для относительного изменения:
$$
\begin{equation}
\varepsilon_{L1}=-\frac {\omega^2 M^2 L_2} {L_1(R_2^2+\omega^2 L_2^2)}.
\label{eps_l1}
\end{equation}
$$
Наконец, изменение активного сопротивления катушки (вносимое активное сопротивление) составляет
$$
\begin{equation}
\Delta R_1=\frac {\omega^2 M^2 R_2} {R_2^2+\omega^2 L_2^2}.
\label{delta_r1}
\end{equation}
$$
Заметим, что отношение изменения индуктивности катушки к изменению активного сопротивления зависит только от параметров объекта (собственных индуктивности и активного сопротивления). Действительно, разделив \eqref{delta_l1} на \eqref{delta_r1}, получим
$$
\frac {\Delta L_1} {\Delta R_1} = - \frac {\cancel{\omega^2 M^2} L_2} {\cancel{R_2^2+\omega^2 L_2^2}} \frac {\cancel{R_2^2+\omega^2 L_2^2}} {\cancel{\omega^2 M^2} R_2}=
- \frac {L_2} {R_2}.
$$
Данное соотношение может быть полезно для реализации функции различения объектов по типу материала, из которого они изготовлены.
Для решения вопроса о выборе оптимальной частоты, рассмотрим, как от частоты зависит отклик катушки на проводящий предмет. Под откликом будем понимать относительное изменение индуктивности катушки металлоискателя по модулю. В соответствии с \eqref{eps_l1} имеем
$$
\begin{equation}
|\varepsilon_{L1}|=\frac {\omega^2 M^2 L_2} {L_1(R_2^2+\omega^2 L_2^2)}.
\label{me_l1}
\end{equation}
$$
Частоту выгодно выбрать так, чтобы отклик был максимальным. Из \eqref{me_l1} видим, что при крайне низких частотах отклик стремится к нулю. С ростом частоты происходит монотонный рост отклика, который стремится к предельному значению \(|\varepsilon_{L1}|_{max}=M^2/(L_1 L_2)\),
$$
|\varepsilon_{L1}| \to \frac {M^2} {L_1 L_2} \text{ при } \omega \to \infty.
$$
Таким образом, выгодно использовать достаточно высокие рабочие частоты. Практически, отклик можно считать достигшим предельного значения, когда начинает выполняться условие
$$
\begin{equation}
\omega^2 L_2^2 \gg R_2^2,
\label{cond_w1}
\end{equation}
$$
дальнейшее увеличение частоты не будет сопровождаться сколь либо значимым ростом отклика.
Понятно, что для объектов из разных материалов, разных по форме и размерам, параметры \(L_2, R_2\) будут разными, соответственно и для оптимальной частоты будем получать разные значения. Но, поскольку с ростом частоты отклик только возрастает, при выборе частоты следует ориентироваться на объекты (из числа тех, которые мы хотим обнаружить), требующие максимальной частоты. Остальные объекты, для которых возможен выбор более низкой рабочей частоты, тем более попадут в зону эффективных рабочих частот.
В то же время, не стоит выбирать слишком высокую частоту, намного большую той, которую даёт условие \eqref{cond_w1}.
Наоборот, рабочую частоту в хороших металлоискателях с высокой чувствительностью стараются сделать как можно более низкой. Обычно предусмотрено переключение частоты для выбора минимальной частоты, подходящей для решения текущей поисковой задачи. Стремление использовать низкие рабочие частоты объясняется тем, что при высокой чувствительности начинает проявляться влияние грунта. Как и в случае с полезными объектами, влияние грунта можно представить воздействием некоторого эквивалентного замкнутого контура со своими значениями собственной индуктивности и активного сопротивления. Только величина R2 для грунта оказывается очень большой (по сравнению с полезными целями), так что в обычных условиях для грунта выполняется соотношение \(\omega^2 L_2^2 \ll R_2^2\) и поэтому величина отклика на грунт может быть приближённо выражена как
$$
|\varepsilon_{L1}| \approx \frac {\omega^2 M^2 L_2} {R_2^2 L_1},
$$
она оказывается пропорциональной квадрату рабочей частоты. Строго говоря, это не совсем верно, так как и индуктивность, и сопротивление зависят от частоты. Впрочем, это более характерно для металлических объектов (для предметов из материалов с высокой удельной проводимостью). А для грунта с его невысокой удельной проводимостью, пропорциональность влияния квадрату рабочей частоты выполняется с высокой точностью.
Итак, мы получили, что с ростом частоты, отклик на полезные цели сначала растёт, а затем достигает "насыщения". Дальнейший рост частоты не приводит к существенному росту отклика, в то время как мешающее поиску влияние грунта продолжает быстро возрастать.
Для достижения высокой чувствительности металлоискателя, отклик на грунт необходимо минимизировать, а значит, рабочая частота должна выбираться по возможности низкой (достаточно высокой для эффективного поиска интересующих нас объектов, но не сверх того).
Отметим, что низкие частоты хорошо подходят для поиска на большой глубине. Как покажем дальше, с увеличением расстояния до объекта, отклик от него резко уменьшается: он обратно пропорционален 6-й степени расстояния. Поэтому от металлоискателя требуется максимальная чувствительность, для достижения которой влияние грунта необходимо сделать минимальным. На большой глубине, даже при очень высокой чувствительности, возможно обнаружение только крупных предметов. И это прекрасно согласуется с тем, что как увидим далее, чем крупнее объект, тем ниже может быть выбрана рабочая частота. На низких частотах не только ослабевает влияние грунта, но и уменьшается отклик на мелкие предметы (для которых минимальная рабочая частота оказывается много выше, чем для крупных предметов). Таким образом, переход на низкие частоты, также уменьшает помехи со стороны малых объектов, которые могут залегать на небольшой глубине и мешать глубинному поиску.
Мы рассмотрели зависимость отклика от частоты на качественном уровне. К сожалению, вычисление конкретного значения рабочей частоты для различных объектов сопряжено со значительными трудностями, которые обусловлены сложностью оценки эквивалентной индуктивности и активного сопротивления объекта. Особенно проблематичен расчёт активного сопротивления объекта.
Как известно, вследствие поверхностного эффекта, вихревые токи в объекте будут сосредоточены преимущественно вблизи поверхности. И если для расчёта индуктивности, мы можем принять толщину слоя с токами стремящейся к нулю, то для расчёта активного сопротивления этот приём абсолютно неприемлем. В данном случае требуется точно знать закон распределения плотности тока по объёму объекта.
Что касается индуктивности, то оказывается, что если даже на самом деле вихревые токи проникают в объект на значительную глубину, расчёт в предположении о концентрации токов в поверхностном слое не приводит к слишком большим погрешностям. Таким образом, оценить индуктивность объекта существенно проще.
Расчёт оптимальной рабочей частоты будет рассмотрен позже, в статье посвящённой численному анализу вихревых токов в проводящих объектах. Здесь будет лишь приведено несколько конкретных примеров, смотрите далее ("Примеры расчёта").
Будем считать, что рабочая частота металлоискателя выбрана должным образом, так что отклик на интересующие нас объекты может быть рассчитан как
$$
\begin{equation}
|\varepsilon_{L1}|_{max}=\frac {M^2} {L_1 L_2}.
\label{el1_lim}
\end{equation}
$$
Для определения величины отклика от воздействия предмета требуется определить значения M, L1, L2. Здесь L1, начальная индуктивность катушки, зависит только от конструкции самой катушки. L2 зависит от формы, размеров предмета и в небольшой степени - от частоты. M зависит и от параметров катушки, и от формы и размеров предмета, и от взаимного расположения катушки и предмета. Для определённости, чтобы получить конкретные соотношения, необходимо выбрать некоторую "стандартную" форму предмета.
Для оценки возможностей металлоискателей традиционно рассматривается их чувствительность по отношению к монетам.
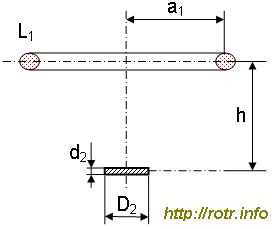
Рис. %img:lc
Пусть монета и катушка расположены соосно (рис. %img:lc). В таком случае мы определим максимальный отклик на монету. Если ось монеты находится под углом к оси катушки (плоскость монеты не параллельна плоскости катушки), или монета находится в стороне от оси катушки, то взаимная индуктивность и, соответственно, величина отклика уменьшаются. По правде говоря, взаимная индуктивность не всегда наибольшая, когда монета и катушка соосны. Например, если монета находится в плоскости катушки, взаимная индуктивность больше, когда монета смещена от центра и расположена ближе к контуру катушки (к проводу, где магнитное поле самое сильное). Однако, уже при минимальном удалении от плоскости катушки, этот эффект ослабевает и исчезает. Поэтому в целом, отклик на объекты, находящиеся на оси катушки, можно использовать для оценки максимального отклика.
Будем считать, что вихревые токи монеты сосредоточены вблизи её края (текут вдоль гурта монеты), образуя тонкий ободок, т.е. кольцо малой ширины (b2 на рисунке %img:coin). Ширина кольца зависит от глубины проникновения вихревых токов в монету, которая связано с частотой внешнего переменного магнитного поля. Эта ширина при оптимальных частотах, как правило, довольно мала - меньше толщины или порядка толщины монеты. Так как токи в монете сосредоточены в узком кольце, то эквивалентная индуктивность монеты может быть рассчитана как индуктивность этого кольца.
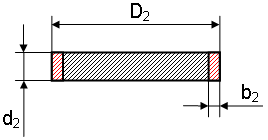
Рис. %img:coin
На рисунке %img:coin изображено сечение монеты. Толщина монеты обозначена как d2, диаметр монеты D2. Кольцо, в котором в основном сосредоточены вихревые токи, выделено цветной штриховкой, его ширина обозначена как b2. Будем считать, что область выбрана таким образом, что токами вне её можно пренебречь ввиду их малости и малого влияния на катушку металлоискателя.
Взаимную индуктивность катушки и монеты вычислим как отношение магнитного потока через монету, создаваемого катушкой, к току в катушке
$$
M = \frac {\Phi_{21}} {i_1}.
$$
Магнитный поток будем рассчитывать исходя из предположения о том, что монета не слишком велика и в её пределах магнитное поле катушки можно считать однородным. Тогда
$$
\Phi_{21}=B_{21} S_2, \\
S_2 = \frac {\pi D_2^2} 4.
$$
Здесь B21 - магнитная индукция поля, создаваемого катушкой в области расположения монеты, например, в точке на оси (поскольку считаем поле катушки однородным в пределах монеты); S2 - площадь монеты (площади аверса или реверса монеты); D2 - диаметр монеты. Записывая выражение для магнитного потока, мы учли, что в нашем случае вектор индукции направлен перпендикулярно плоскости монеты.
Магнитная индукция на оси кругового тока, как известно из курса общей физики, равна
$$
B_{21}=\frac {\mu \mu_0 i_1 a_1^2} {2 (a_1^2+h^2)^{3/2}},
$$
i1 - сила тока в витке; a1 - радиус витка; h - расстояние от центра витка до точки на оси, где вычисляется магнитная индукция B21. Под B21 здесь понимается проекция вектора \(\vec B_{21}\) на ось витка. В точках, лежащих на оси витка, только эта проекция отлична от нуля. Индексы в обозначении B21 указывают на то, что поле создаётся витком (индекс 1) и величина относится к точке в области расположения монеты (индекс 2). Сила тока - алгебраическая величина (со знаком), ток считаем положительным, если он совпадает с направлением обхода контура (витка). Для выбора направления обхода, выбираем удобное для нас направление оси, тогда направление обхода должно образовывать правовинтовую систему с осью.
Если катушка имеет n1 компактно размещённых витков, то её поле будет таким же, как поле одного витка с током в n1 раз больше:
$$
B_1=\frac {\mu \mu_0 i_1 n_1 a_1^2} {2 (a_1^2+h^2)^{3/2}},
$$
считая магнитную проницаемость среды равной 1, получаем
$$
B_1 = \frac {\mu_0 i_1 n_1 a_1^2} {2 (a_1^2+h^2)^{3/2}}.
$$
Итак, с учётом выше сказанного,
$$
\Phi_{21}=\frac {\mu_0 i_1 n_1 a_1^2} {2 (a_1^2+h^2)^{3/2}} \frac {\pi} {4} D_2^2 \approx \\
\approx \frac {\mu_0 i_1 n_1 a_1^2 D_2^2} {2.546 (a_1^2+h^2)^{3/2}}, \\
M=\frac {\Phi_{21}} {i_1} \approx \frac {\mu_0 n_1 a_1^2 D_2^2} {2.546 (a_1^2+h^2)^{3/2}}.
$$
Для вычисления отклика на монету по формуле \eqref{el1_lim}, осталось определить L1 и L2. Для вычисления индуктивностей, воспользуемся приближёнными формулами из справочной литературы (например, смотрите [%link:calc_l]).
Катушку металлоискателя будем считать круговой с круглым сечением, её индуктивность
$$
L_1=\mu_0 n_1^2 a_1 k_1,
$$
где n1 - количество витков; a1 - средний радиус; k1 - коэффициент, зависящий от форм-фактора катушки \(\gamma_1=r_1/(2a_1)\) (r1 - радиус сечения катушки),
$$
k_1 \approx \left(1+\frac {\gamma_1^2} 2\right) \ln \frac 4 \gamma_1 - 1.75 + \frac {\gamma_1^2} 6.
$$
С изменением соотношения \(r_1/(2a_1)\), коэффициент k1 изменяется довольно медленно, поэтому зададимся конкретным значением соотношения для вычисления L1, а полученный результат обобщим на произвольные катушки. При этом потеряем в точности, но приблизительные оценки выполнить сможем (изменение форм фактора от 0.001 до 0.1, т.е. на два порядка, приводит к изменению коэффициента k1 от примерно 6.5 до примерно 2.0, это изменение чуть более чем в 3 раза - остаёмся в пределах одного порядка). Важно, что благодаря приближению, получим простые соотношения, пригодные для дальнейшего анализа и дающие важную информацию об основных закономерностях.
Пусть \(r_1/(2a_1) \approx 0.01\), тогда индуктивность катушки
$$
\begin{equation}
L_1 \approx 4.242 \mu_0 n_1^2 a_1.
\label{l_eq}
\end{equation}
$$
Индуктивность монеты вычисляем как индуктивность кругового кольца прямоугольного сечения,
$$
L_2 \approx \mu_0 a_2 \left( \ln \frac {8 a_2} {d_2+b_2} - 0.5 \right),
$$
где a2 - радиус кольца (считаем равным радиусу монеты); d2 - толщина кольца (толщина монеты); b2 - ширина кольца (ширина области, в которой сосредоточен основной вихревой ток).
Мы предполагаем, что \( b_2 \ll d_2 \). Получим, что результат зависит от соотношения диаметра и толщины монеты. Для простоты будем считать, что соотношение для типичной монеты постоянно (например, пусть оно такого порядка, как для монеты 5 коп. СССР, у которой диаметр составляет 12.5 мм, толщина 1.5 мм). Даже если это не так, за счёт того, что выражение находится под логарифмом, зависимость индуктивности от него получается "слабой". Таким образом,
$$
L_2 \approx 3.700 \mu_0 a_2 \approx
1.850 \mu_0 D_2,
$$
D2 - диаметр монеты.
Подставляя выражения для индуктивности катушки и монеты и их взаимной индуктивности в формулу для вычисления величины отклика, получаем
$$
|\varepsilon_{L1}| \approx \frac {M^2} {L_1 L_2}=\frac {\mu_0^2 n_1^2 a_1^4 D_2^4} {2.546^2 (a_1^2+h^2)^3}
\frac 1 {4.242 \mu_0 n_1^2 a_1}
\frac 1 {1.850 \mu_0 D_2} \approx \\
\approx \frac {a_1^3 D_2^3} {50.87 (a_1^2+h^2)^3}.
$$
Итак, отклик на монету может быть оценён как
$$
\begin{equation}
|\varepsilon_{L1}| \approx \frac {a_1^3 D_2^3} {50.87 (a_1^2+h^2)^3}.
\label{e_tot}
\end{equation}
$$
Следует иметь в виду, что постоянная 50.87 в формуле, на самом деле не вполне постоянная, а является коэффициентом, в некоторой степени зависящим от конструкции катушки, формы и размеров объекта. Но для приближённых вычислений (особенно для оценки порядков величин) этой зависимостью можно пренебречь. Если точность результата не устраивает, всегда можно вернуться к исходному выражению \eqref{el1_lim} и подставить в него уточнённые значения M, L1, L2. Кроме того, индуктивность L1 может быть непосредственно измерена, если имеется уже изготовленная катушка.
Для отклика на монету мы получили формулу
$$
\begin{equation}
|\varepsilon_{L1}| \approx \frac {a_1^3 D_2^3} {50.87 (a_1^2+h^2)^3}.
\label{cresp}
\end{equation}
$$
Рассмотрим, какие из неё следуют выводы.
Зависимость отклика от глубины.
Как видим, отклик зависит от расстояния от центра катушки до объекта h. Чем расстояние (или глубина) больше, тем слабее отклик. При малых глубинах, пока \(h^2 \ll a_1^2\), падение отклика с увеличением глубины сравнительно медленное, но затем оно ускоряется и, начиная с h, примерно равного диаметру катушки, т.е. 2*a1, отклик становится практически обратно пропорциональным 6-й степени глубины:
$$
|\varepsilon_{L1}| \approx \frac {a_1^3 D_2^3} {50.87 h^6} \text{ при} \\
h^2 \gg a_1^2.
$$
Это объясняет высокую сложность существенного увеличения глубины поиска у металлоискателя. Так, для увеличения максимальной глубины поиска вдвое, порог чувствительности прибора к изменению индуктивности катушки должен быть снижен более чем в 60 раз. Это довольно трудная задача, особенно с учётом усиления влияния нежелательных отклонений параметров катушки под действием различных дестабилизирующих факторов (деформация из-за перепадов температуры или механических нагрузок, влияние грунта и др.).
Максимальным отклик будет при очень малых глубинах залегания объекта
$$
|\varepsilon_{L1}| \approx \frac 1 {50.87} \left( \frac {D_2} {a_1} \right)^3 \text{ при} \\
h^2 \ll a_1^2.
$$
Этим соотношением определяется минимальный размер в принципе ещё обнаружимых предметов, который зависит от чувствительности прибора и размера катушки:
$$
D_2 \approx a_1 \cdot \sqrt[3]{50.87 |\varepsilon_{L1}|}.
$$
Чем катушка больше, тем больше должен быть размер предмета, чтобы прибор данной чувствительности был способен его обнаружить; зависимость прямо пропорциональная. Наоборот, металлоискатель с маленькой катушкой способен обнаружить мелкие объекты. Но только вблизи к поверхности, с увеличением глубины величина отклика стремительно падает.
Зависимость отклика от размеров объекта.
Отклик на монету пропорционален третьей степени её диаметра, т.е. довольно быстро растёт с увеличением размеров объекта. И быстро падает с уменьшением размеров, что создаёт трудности с поиском очень малых объектов, для обнаружения которых требуется увеличивать чувствительность прибора и/или уменьшать размеры катушки (но с уменьшением размеров катушки быстро падает максимальная глубина поиска).
Для очень больших предметов соотношение \(|\varepsilon_{L1}|\sim D_2^3\) перестаёт выполняться и с дальнейшим ростом размеров, увеличение отклика сначала замедляется, затем практически прекращается. Это объясняется тем, что формула для величины отклика выводилась в предположении о малости объекта, так чтобы поле катушки в пределах объекта можно было считать практически однородным. Если же предмет большой, в его областях, более удалённых от центра катушки, магнитное поле оказывается намного слабее и вызываемые им вихревые токи намного меньше. В дополнение к этому, создаваемое вихревыми токами поле от более удалённых областей, будет оказывать меньшее влияние на катушку. Поэтому, как бы ни был велик объект, его "эффективный" размер оказывается ограниченным. Кстати, это объясняет существование теоретической предельной глубины обнаружения. На большей глубине прибор с данной чувствительностью и катушкой не сможет ничего обнаружить в принципе, даже бесконечно большой объект.
Зависимость отклика от размеров катушки.
Радиус катушки входит как в числитель, так и в знаменатель выражения \eqref{cresp}, в связи с чем, зависимость отклика от размера катушки оказывается неоднозначной. Поведение отклика как функции от радиуса катушки можно исследовать, вычислив производную отклика по радиусу. Получим следующее.
Если глубина (расстояние до предмета) мала, меньше радиуса катушки, то с увеличением радиуса отклик уменьшается.
Если глубина больше радиуса катушки, с увеличением радиуса отклик увеличивается.
Отклик максимален, когда радиус катушки равен глубине. Впрочем, данный вывод имеет малую практическую ценность, так как обычно глубина залегания предмета заранее неизвестна.
Выбирать радиус катушки следует исходя из желаемой максимальной глубины поиска и минимального размера обнаруживаемых предметов. Чем больше катушка, тем большей получается максимальная глубина поиска, но меньше отклик на любые объекты (значит обнаружить можно только крупные, мелкие не будут "видны", даже если они находятся на поверхности). Чем меньше радиус катушки, тем больше отклик на объекты, значит, могут быть обнаружены даже очень малые предметы, но только вблизи поверхности - у маленькой катушки оказывается очень малой максимальная глубина поиска; на большой глубине не будут найдены даже очень крупные объекты (уменьшается глубина, начиная с которой отклик становится обратно пропорциональным её 6-й степени).
Рассмотрим несколько примеров для реальных монет, чтобы получить представление о порядке величины отклика.
В качестве объектов поиска рассмотрим две монеты: 5 копеек СССР и 1 копейка СССР. Размеры монет будем считать равными:
5 коп.: диаметр 25 мм, толщина 1.5 мм;
1 коп.: диаметр 15 мм, толщина 0.9 мм;
пусть материал монет - латунь, удельную проводимость которой примем равной 13*106 1/(Ом*м).
В таблице сведены результаты, полученные разными способами:
рассчитанные по формуле \eqref{e_tot},
$$
|\varepsilon_{L1}| \approx \frac {a_1^3 D_2^3} {50.87 (a_1^2+h^2)^3};
$$
вычисленные путём численного анализа вихревых токов;
измеренные на экспериментальной установке.
| h, см |
\(\varepsilon\), по формуле |
\(\varepsilon\), численный анализ |
\(\varepsilon\), измерения |
| 5 коп. |
| 0 |
8.1e-4 |
8.0e-3 |
1.1e-3 |
| 3.5 |
4.3e-4 |
4.1e-4 |
5.6e-4 |
| 4.5 |
3.0e-4 |
2.9e-4 |
3.1e-4 |
| 8.5 |
6.0e-4 |
5.7e-5 |
8.7e-5 |
| 1 коп. |
| 0 |
1.7e-4 |
1.9e-4 |
2.1e-4 |
| 3.5 |
0.9e-4 |
1.0e-4 |
1.0e-4 |
Параметры используемого оборудования: небольшая катушка с диаметром 145 мм (a1 = 72.5 мм) и индуктивностью 0.20 мГн; катушка включена в состав прибора, работающего на основе измерения частоты. Рабочая частота выбрана заведомо высокой, примерно 110 кГц.
Как видим из таблицы, полученная нами формула для расчёта отклика вполне подходит для оценочных расчётов. Расхождения с опытными данными частично можно объяснить погрешностями измерений, сложностью точного позиционирования объекта (монеты).
Для того чтобы иметь представление о примерных значениях рабочей частоты для поиска различных объектов, забегая вперёд, приведём некоторые данные, которые могут быть получены с помощью численного моделирования.
Для тех же самых монет получим следующие результаты для рабочей частоты (определяется из условия получения отклика на уровне 0.8 от предельного значения, достигаемого на высоких частотах):
5 коп.: fmin = 20 кГц;
1 коп.: fmin = 56 кГц.
Таким образом, если мы ищем объекты типа 5 коп. и крупнее, нам подойдёт рабочая частота около 20 кГц или выше. Если хотим обеспечить эффективный поиск, начиная с объектов типа 1 коп., следует выбирать рабочую частоту порядка 50..60 кГц или выше. Но слишком высокой рабочую частоту делать не стоит из-за увеличения влияния грунта с ростом частоты, в то время как значимого роста отклика на полезные объекты происходить не будет. В то же время, работать на более низких частотах вполне возможно, так как падение отклика оказывается не слишком большим даже при снижении частоты в несколько раз (относительно значений, указанных здесь для уровня отклика 0.8 от предельного значения).
Если бы монеты были медные (проводимость примем равной 56*106 1/(Ом*м), проводимость может варьироваться в небольших пределах в зависимости от степени чистоты металла и способа обработки), то получили бы значения 4.6 кГц и 13 кГц соответственно, т.е. для поиска предметов из хорошо проводящих материалов могут использоваться более низкие частоты.
Как видим, рабочая частота должна выбираться исходя из минимальных размеров предметов, которые требуется найти и проводимости материала, из которого предметы изготовлены. Чем больше размеры и чем выше проводимость материала, тем ниже может быть выбрана частота.
Для очень мелких объектов требуются высокие рабочие частоты. Так, например, для поиска медных крупинок с размерами около 1 мм рабочая частота оказывается порядка 950 кГц; для серебряных крупинок - в районе 850 кГц; золотых - около 1.2 МГц (указаны частоты, на которых отклик на данные объекты достигает уровня 0.8 от предельного значения).
Такие высокие частоты не используются в обычных металлоискателях, но, к счастью, в данном случае, значительное уменьшение частоты не приводит к слишком сильному снижению отклика. В рассмотренном выше примере, при снижении рабочей частоты до значений порядка 100 кГц, величина отклика уменьшится примерно в 2 раза.
%link:calc_l. "Калантаров П. Л., Цейтлин Л. А. Расчёт индуктивностей: Справочная книга (3-е изд.), 1986.
author: hamper; date: 2020-01-15; modified: 2020-03-16