Умножитель напряжения под нагрузкой. Детализированный анализ
Рассмотрим идеальный умножитель напряжения с чётным коэффициентом m. Ранее мы уже составили уравнения, описывающие процессы в умножителе, но использовали при этом достаточно грубые приближения ("Умножитель напряжения под нагрузкой"). В данном случае будем анализировать процессы в умножителе более детализировано и покажем, что в результате придём к тем же самым уравнениям.
Будем рассматривать умножитель на протяжении одного такта работы, т.е. на протяжении одного периода колебаний напряжения источника питания. Каждый такт состоит из двух равных по длительности полутактов, на одном из которых происходит передача заряда от нечётных конденсаторов к чётным, а на другом - наоборот, при этом происходит постепенный перенос заряда от звена к звену, от начала цепочки к её концу. В свою очередь, в каждом из полутактов можно выделить две части - пассивную фазу в начале полутакта, когда все диоды закрыты и активную фазу, когда собственно и происходит переключение диодов и передача зарядов между конденсаторами.
Ранее мы считали, что активная фаза очень кратковременна и пренебрегали её длительностью. Это можно считать справедливым для крайне малых токов нагрузки, но в общем случае, длительность активной фазы может быть сопоставима с длительностью пассивной и даже превышать её.
Пусть длительность пассивной фазы, т.е. промежуток времени, когда все диоды закрыты - от начала полутакта до момента, когда открывается один из диодов умножителя, равен \(\theta.\) Время, в течение которого один диод находится в открытом состоянии обозначим \(\theta_1.\) Как уже неоднократно было показано, диоды в активной фазе полутакта открываются поочерёдно, по одному, начиная с конца схемы и далее по направлению к началу (понятно, что в зависимости от полутакта будут открываться только нечётные или только чётные диоды). В действительности, интервал времени, в течение которого разные диоды находятся в открытом состоянии отличаются, но эти отличия много меньше длительности полутакта и в любом случае данное приближение будет более точным, чем использовавшееся ранее, когда считалось, что \(\theta_1=0.\) Правомерность такого приближения также подтверждается результатами моделирования умножителей.
Кроме того, будем считать, что \(\theta, \theta_1\) одинаковы для обоих полутактов работы умножителя. Данные величины связаны соотношением
$$
\theta+\frac m 2 \theta_1=\frac T 2; \theta_1=\frac{T-2\theta}m.
\tag{1}
$$
Данные выражения отражают тот факт, что полутакт образован активной и пассивной фазами, причём длительность пассивной составляет \(\theta_1 m/2,\) где m/2 - количество диодов, принимающих участие в данном полутакте (половина от общего количества).
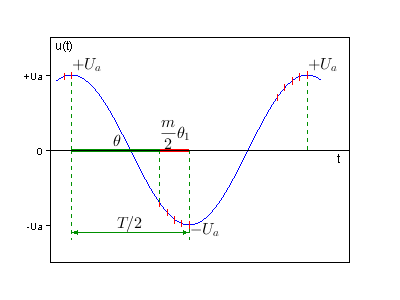
Рис. %img:i1
На рис. %img:i1 изображён график питающего напряжения, на котором отмечены основные события на протяжении одного такта работы умножителя. За начало такта мы принимаем момент, когда мгновенное напряжение источника достигает положительного амплитудного значения, u(t)=+Ua. После прохождения этой точки все диоды умножителя будут находиться в закрытом состоянии на протяжении промежутка времени \(\theta.\) Затем следует активная фаза полутакта, которая начинается в момент, когда открывается диод Dm-1. Через промежуток времени, равный \(\theta_1\), данный диод закрывается и открывается Dm-3 и т.д., до диода D1, который открывается за время \(\theta_1\) до момента завершения полутакта и закрывается вместе с завершением данного полутакта. Это происходит, когда напряжение источника питания достигает отрицательного амплитудного значения, u(t)=-Ua. На рисунке моменты переключения диодов отмечены красными засечками. Левая соответствует началу активной фазы данного полутакта, когда открывается диод, вступающий в работу первым, правая соответствует концу полутакта. Средние соответствуют моментам, когда закрывается соответствующий диод и открывается предшествующий ему.
В момент, когда u(t)=-Ua, начинается второй полутакт. Его активная фаза начинается в момент перехода в отрытое состояние диода Dm. Затем открывается Dm-2, а Dm закрывается и т.д., до диода D2, который открывается последним, а закрывается он в момент завершения данного полутакта и такта в целом. После этого начинается следующий такт работы умножителя.

Рис. %img:i2
Прежде всего, составим уравнения для первого полутакта. Напряжения на конденсаторах умножителя в начале полутакта (и в начале такта) обозначим как Ui, где i=1, 2, ..., m. Напряжения в конце полутакта обозначим как U'i. Нам потребуется знать моменты времени, когда в данном полутакте закрывается каждый из диодов. В первом полутакте работают нечётные диоды Dj, j=1, 3, ..., m-1. Промежуток времени от начала полутакта до перехода диода Dj в закрытое состояние составляет:
$$
j=1: \frac T 2, \\
j=3: \frac T 2 -\theta_1, \\
j=5: \frac T 2 -2\theta_1, \\
(j): \frac T 2 -\frac{j-1}2 \theta_1.
\tag{2}
$$
Первым закрывается диод Dm-1 через время от начала полутакта, равное
$$
\frac T 2 -\frac{m-2}2 \theta_1=\frac T 2-\frac m 2 \theta_1+\theta_1=\theta+\theta_1.
\tag{3}
$$
Итак, промежуток времени от начала полутакта до момента перехода диода Dj в закрытое состояние составляет
$$
\tau_j=\frac T 2 -\frac{j-1}2 \theta_1.
\tag{4}
$$
От данного момента до конца полутакта остаётся время
$$
\chi_j=\frac T 2-\tau_j=\frac{j-1}2 \theta_1.
\tag{5}
$$
Теперь перейдём, собственно, к составлению уравнений. Прежде всего, заметим, что к концу первого полутакта конденсатор C1 зарядится до амплитудного значения напряжения питающего источника, U'1=Ua. Конденсатор Cm на протяжении всего первого полутакта разряжается током нагрузки I:
$$
U'_1=U_a, \\
U'_m=U_m-\frac I C \frac T 2=U_m-\gamma\frac T 2=U_m-\Delta U,
\tag{6}
$$
здесь используются следующие обозначения
$$
\gamma=\frac I C,
\tag{7}
$$
$$
\Delta U=\gamma \frac T 2,
\tag{8}
$$
\(\Delta U\) - падение напряжения на конденсаторе за половину периода (за время одного полутакта) в результате протекания тока нагрузки.
В момент перехода диода Dj, j=3, 5, ..., m-1 в закрытое состояние выполняются равенства
$$
U'^*_{j-1}=U'^*_j,
\tag{9}
$$
где через U'*j, очевидно, обозначаем напряжение на конденсаторе Cj в указанный момент времени. Подробно об обосновании этих уравнений речь идёт в документе, посвящённом упрощённому варианту вывода уравнений умножителя. Кратко можно объяснить данное равенство тем, что в указанный момент времени диод Dj закрывается, а диод Dj-1 открывается, т.е. напряжение на каждом из этих диодов в данный момент равно 0, а так как названные диоды и два конденсатора образуют замкнутый контур, то напряжения на конденсаторах будут равны.
После рассмотренного момента напряжение на конденсаторе с нечётным номером Cj остаётся неизменным до конца полутакта (он отключается от остальной части цепи закрывшимися к данному моменту диодами), а напряжение на конденсаторе с чётным номером Cj-1 линейно падает в результате протекания тока нагрузки в течение промежутка времени \(\chi_j\)
$$
U'_j=U'^*_j, \\
U'_{j-1}=U'^*_{j-1}-\gamma \frac{j-1}2 \theta_1, \\
j=3, 5, ..., m-1.
\tag{10}
$$
На протяжении всего времени от начала полутакта до момента перехода Dj в закрытое состояние, суммарный заряд конденсаторов Cj-1, Cj уменьшается в результате протекания тока нагрузки (сначала, в течение пассивной фазы, теряет заряд только Cj-1 с чётным номером, а с начала активной фазы - оба конденсатора, так как в ветвь с нечётными конденсаторами ответвляется часть тока нагрузки через один из открытых диодов).
Так что к моменту, когда Dj закроется,
$$
U'^*_{j-1}+U'^*_j=U_{j-1}+U_j-\gamma \left(\frac T 2 - \frac{j-1}2 \theta_1 \right), \\
j=3, 5, ..., m-1,
\tag{11}
$$
а с учётом (9)
$$
U'^*_{j-1}=U'^*_j=\frac 1 2 \left(U_{j-1}+U_j-\gamma \left(\frac T 2-\frac{j-1}2 \theta_1\right) \right), \\
j=3, 5, ..., m-1.
\tag{12}
$$
Подставляя полученные значения в (10), а также учитывая уравнения (6), находим напряжения на конденсаторах в конце полутакта:
$$
\begin{cases}
U'_1=U_a, \\
U'_m=U_m-\Delta U, \\
U'_{j-1}=\frac 1 2 \left( U_{j-1}+U_j-\gamma\left( \frac T 2 -\frac{j-1}2 \theta_1 \right) \right)-\gamma \frac{j-1}2\theta_1, \\
U'_j=\frac 1 2 \left( U_{j-1}+U_j-\gamma\left( \frac T 2 -\frac{j-1}2 \theta_1 \right) \right), \\
j=3, 5, ..., m-1
\end{cases}
$$
или
$$
\begin{cases}
U'_1=U_a, \\
U'_m=U_m-\Delta U, \\
U'_{j-1}=\frac 1 2 (U_{j-1}+U_j-\Delta U)-\frac 1 2 \gamma \frac{j-1}2 \theta_1, \\
U'_j=\frac 1 2 (U_{j-1}+U_j-\Delta U)+\frac 1 2 \gamma \frac{j-1}2 \theta_1, \\
j=3, 5, ..., m-1.
\end{cases}
\tag{13}
$$
Теперь рассмотрим второй полутакт, который начинается в момент, когда u(t)=-Ua, а завершается в момент, когда u(t)=+Ua. Длительность второго полутакта, как и первого, составляет T/2. Напряжения на конденсаторах в начале второго полутакта - это напряжения в конце первого, они равны найденным нами значениям U'i. Напряжения в конце второго полутакта, который также соответствует концу такта в целом, а также является моментом начала следующего такта, обозначим как U''i.
Во время активной фазы второго полутакта работают диоды с чётными номерами Di, i=2, 4, ..., m. Время от начала второго полутакта до момента, когда закроется диод Di составляет
$$
i=2: \frac T 2; \\
i=4: \frac T 2 -\theta_1; \\
i=6: \frac T 2 -2 \theta_1; \\
\ldots; \\
(i): \frac T 2 - \frac{i-2}2 \theta_1; \\
i=m: \frac T 2 -\frac{m-2}2 \theta_1=\theta+\theta_1.
$$
Время от момента, когда диод Di закрывается до конца полутакта (и конца такта в целом) составляет
$$
\frac T 2 -\frac T 2 +\frac{i-2}2 \theta_1=\frac{i-2}2 \theta_1, \\
i=2, 4, \ldots, m.
$$
Составляем уравнения для моментов, когда закрывается диод Di, i=2, 4, ..., m. В случае если i=2,
$$
U''^*_1-U''^*_2=-U_a, \\
U''^*_1+U''^*_2=U'_1+U'_2-\Delta U,
\tag{14}
$$
причём
$$
U_1''=U''^*_1, \\
U_2''=U''^*_2,
\tag{15}
$$
так как момент, когда закрывается D2, совпадает с моментом завершения такта.
Для всех остальных i, i=4, 6, ..., m, уравнения имеют вид:
$$
U''^*_{i-1}-U''^*_i=0, \\
U''^*_{i-1}+U''^*_i=U'_{i-1}+U'_i-\gamma \left(\frac T 2 -\frac{i-2}2 \theta_1 \right), \\
i=4, 6, \ldots, m
$$
или
$$
U''^*_{i-1}-U''^*_i=0, \\
U''^*_{i-1}+U''^*_i=U'_{i-1}+U'_i-\Delta U+\gamma \frac{i-2}2 \theta_1, \\
i=4, 6, \ldots, m,
\tag{16}
$$
откуда получаем
$$
U''^*_{i-1}=U''^*_i=\frac 1 2 (U'_{i-1}+U'_i-\Delta U)+\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
i=4, 6, \ldots, m.
\tag{17}
$$
Тогда напряжения на конденсаторах в конце такта будут равны
$$
U''_{i-1}=U''^*_{i-1}=\frac 1 2 (U'_{i-1}+U'_i-\Delta U)+\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
U''_i=U''^*_i-\gamma \frac{i-2}2 \theta_1=\frac 1 2 (U'_{i-1}+U'_i-\Delta U)-\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
i=4, 6, \ldots, m.
\tag{18}
$$
Подставим в выражения (18) значения для величин с одним штрихом из (13). Учитываем, что i в (18) принимает чётные значения (соответственно, i-1 - нечётные), а j в 13 - нечётные. Будем вычислять напряжения U''j на конденсаторах с чётными номерами, так как сумма этих напряжений равна выходному напряжению умножителя, которое в конечном итоге нам и требуется вычислить.
$$
U''_i=U''^*_i-\gamma \frac{i-2}2 \theta_1=\frac 1 2 (U'_{i-1}+U'_i-\Delta U)-\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
i=4, 6, \ldots, m.
$$
Если пока исключить из рассмотрения индекс со значением i=m, то
$$
i-1=j, j=i-1, \\
U'_{i-1}=\frac 1 2 (U_{i-2}+U_{i-1}-\Delta U)+\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
\\
i=j-1, j=i+1, \\
U'_i=\frac 1 2 (U_i+U_{i+1}-\Delta U)-\frac 1 2 \gamma \frac i 2 \theta_1, \\
i=4, 6, ..., m-2
$$
и
$$
U''_i=\frac 1 2 \left( \frac 1 2 (U_{i-2}+U_{i-1}-\Delta U)+\frac 1 2 \gamma \frac{i-2}2 \theta_1+\frac 1 2 (U_i+U_{i+1}-\Delta U)-\frac 1 2 \gamma \frac i 2 \theta_1-\Delta U \right)-\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
i=4, 6, ..., m-2.
\tag{19}
$$
Исключим из выражений напряжения на конденсаторах с нечётными номерами. Для этого воспользуемся уравнениями (18), из которых следует, что
$$
U''_{i-1}=U''_i+\gamma \frac{i-2}2 \theta_1, \\
i=4, 6, \ldots, m.
\tag{20}
$$
Соотношение (20) выполняется в конце каждого такта, а конец такта совпадает с началом следующего такта. Значит, соотношения (20) выполняется и для момента - начала такта, т.е.
$$
U_{i-1}=U_i+\gamma \frac{i-2}2 \theta_1, \\
i=4, 6, \ldots, m.
$$
или
$$
U_j=U_{j+1}+\gamma \frac{j-1}2 \theta_1, \\
j=3, 5, \ldots, m-1.
\tag{21}
$$
С учётом (21) выражение (19) примет вид:
$$
U''_i=\frac 1 2 \left( \frac 1 2 (U_{i-2}+U_i+\gamma \frac{i-2}2 \theta_1-\Delta U)+\frac 1 2 \gamma \frac{i-2}2 \theta_1+\frac 1 2 (U_i+U_{i+2}+\gamma \frac i 2 \theta_1-\Delta U)-\frac 1 2 \gamma \frac i 2 \theta_1-\Delta U \right)-\frac 1 2 \gamma \frac{i-2}2 \theta_1, \\
i=4, 6, ..., m-2.
$$
или
$$
U''_i=\frac 1 4 U_{i-2}+\frac 1 2 U_i+\frac 1 4 U_{i+2}-\Delta U, \\
i=4, 6, ..., m-2.
\tag{22}
$$
Теперь выразим U''2 и U''m. В соответствии с (14) и (15),
$$
U''_2=\frac 1 2 (U_a+U'_1+U'_2-\Delta U),
$$
из уравнений (13) находим:
$$
U'_1=U_a, \\
U'_2=\frac 1 2 (U_2+U_3-\Delta U)-\frac 1 2 \gamma \theta_1,
$$
тогда
$$
U''_2=U_a+\frac 1 2 \left( \frac 1 2 (U_2+U_3-\Delta U)-\frac 1 2 \gamma \theta_1-\Delta U \right).
$$
Подставляем \(U_3=U_4+\gamma \theta_1\) (в соответствии с (21))
$$
U''_2=U_a+\frac 1 4 U_2+\frac 1 4 U_4-\frac 3 4 \Delta U.
\tag{23}
$$
Осталось найти Um. В соответствии с (18)
$$
U''_m=\frac 1 2 (U'_{m-1}+U'_m-\Delta U)-\frac 1 2 \gamma \frac{m-2}2 \theta_1,
$$
из (13) имеем
$$
U'_{m-1}=\frac 1 2 (U_{m-2}+U_{m-1}-\Delta U)+\frac 1 2 \gamma \frac{m-2}2 \theta_1, \\
U'_m=U_m-\Delta U.
$$
Согласно с (21),
$$
U_{m-1}=U_m+\gamma \frac{m-2}2 \theta_1.
$$
Тогда
$$
U''_m=\frac 1 2 \left( \frac 1 2 (U_{m-2}+U_m+\gamma \frac{m-2}2\theta_1-\Delta U)+\frac 1 2 \frac{m-2}2 \theta_1+U_m-\Delta U-\Delta U \right)-\frac 1 2 \gamma \frac{m-2}2 \theta_1.
$$
Окончательно имеем
$$
U''_m=\frac 1 4 U_{m-2}+\frac 3 4 U_m-\frac 5 4 \Delta U.
\tag{24}
$$
Объединяя уравнения (22), (23), (24), окончательно получаем следующую систему:
$$
\begin{cases}
U''_2=U_a+\frac 1 4 U_2+\frac 1 4 U_4-\frac 3 4 \Delta U, \\
U''_i=\frac 1 4 U_{i-2}+\frac 1 2 U_i+\frac 1 4 U_{i+2}-\Delta U, \\
i=4, 6, ..., m-2, \\
U''_m=\frac 1 4 U_{m-2}+\frac 3 4 U_m-\frac 5 4 \Delta U.
\end{cases}
\tag{25}
$$
Как видим, полученная система уравнений полностью совпадает с системой, полученной при рассмотрении процессов в умножители в грубом приближении (документ "Умножитель напряжения под нагрузкой"). Таким же будет и решение системы. Относительно напряжений на конденсаторах с чётными номерами:
$$
U_{2n+2}=2U_a+\Delta U(2n^2+n-2nm-m), \\
n=0, 1, 2, \ldots, (m-2)/2, \\
(U_2, U_4, \ldots, U_m).
\tag{26}
$$
Выходное напряжение умножителя
$$
U_{out}=mU_a-\frac I{2FC}\left(\frac{m^3}6+\frac{m^2}8+\frac m{12}\right),
\tag{27}
$$
m - коэффициент умножения;
Ua - амплитуда питающего напряжения;
I - ток нагрузки;
F - частота переменного тока питающего источника;
C - ёмкость конденсаторов в умножителе.
Формулы дают значения для пиковых значений напряжений (в точках максимума пульсаций выходного напряжения).
Размах пульсаций выходного напряжения умножителя - это разность между максимальным и минимальным мгновенным значением выходного напряжения. Максимальное, пиковое значение было найдено в предыдущем пункте документа и может быть вычислено по формуле (27). Минимальное значение выходного напряжения достигается в момент, предшествующий началу активной фазы второго (в нашем анализе) полутакта, т.е. через промежуток времени \(\theta\) после начала второго полутакта: к концу первого полутакта напряжения на конденсаторах с чётными номерами падают из-за того, что от них происходит подзаряд конденсаторов с нечётными номерами, кроме того происходит разряд конденсаторов током нагрузки; затем, за счёт тока нагрузки, напряжение продолжает падать вплоть до начала активной фазы второго полутакта.
Если обозначать напряжения на конденсаторах в начале такта как Ui, в конце первого полутакта как U'i, то, как было установлено в предыдущем пункте,
$$
U'_i=\frac 1 2 (U_i+U_{i+1}-\Delta U)-\frac 1 2 \gamma \frac i 2 \theta_1, \\
i=2, 4, \ldots, m-2, \\
U'_m=U_m-\Delta U,
\tag{28}
$$
здесь \(\gamma=I/C, \Delta U=\gamma T/2\); I - ток нагрузки; C - ёмкость конденсатора (в рассматриваемом случае все конденсаторы умножителя имеют одинаковую ёмкость); T - период колебаний питающего напряжения; \(\theta_1\) - время переключения (время, в течение которого диод находится в открытом состоянии в процессе переключений), считаем, что величина одинакова для всех звеньев умножителя и \(\theta_1=(T/2-\theta)/(m/2)\); \(\theta\) - длительность пассивной фазы полутакта (в начале полутакта, когда все диоды закрыты).
Используя (21), можем исключить из выражения (28) напряжения на нечётных конденсаторах:
$$
U_j=U_{j+1}+\gamma \frac{j-1}2 \theta_1, \\
j=3, 5, \ldots, m-1, \\
U'_i=\frac 1 2 \left( U_i+U_{i+2}+\gamma \frac i 2 \theta_1-\Delta U \right)-\frac 1 2 \gamma \frac i 2 \theta_1, \\
i=2, 4, \ldots, m-2
$$
или
$$
\begin{cases}
U'_i=\frac 1 2 (U_i+U_{i+2}-\Delta U), \\
i=2, 4, \ldots, m-2, \\
U'_m=U_m-\Delta U.
\end{cases}
\tag{29}
$$
Значения напряжений, вычисляемые по данным формулам, соответствуют моменту завершения первого полутакта и начала второго. После этого момента ещё в течение всей пассивной фазы второго полутакта напряжения на конденсаторах с чётными номерами будет падать за счёт тока нагрузки, так что минимальные напряжения на этих конденсаторах составят
$$
U^*_k=U'_k-\gamma \theta,
$$
то есть
$$
\begin{cases}
U^*_i=\frac 1 2 (U_i+U_{i+2}-\Delta U)-\gamma \theta, \\
i=2, 4, \ldots, m-2, \\
U^*_m=U_m-\Delta U-\gamma \theta.
\end{cases}
\tag{30}
$$
В ходе упрощённого анализа использовались соотношения
$$
U^*_i=\frac 1 2 (U_i+U_{i+2}-\Delta U)-\Delta U, i=2, 4, \ldots, m-2, \\
U^*_m=U_m-2\Delta U, \\
\tag{31}
$$
которые привели к результату
$$
h=\Delta U\left(\frac{m^2}4+\frac m 2\right).
\tag{32}
$$
Эти соотношения являются частным случаем (30), когда \(\theta \rightarrow T/2.\) В действительности же, длительность пассивной фазы полутакта меньше половины периода и размах пульсаций будет также несколько меньше значения, даваемого формулой (32) и составит, очевидно,
$$
h=\Delta U\frac{m^2}4+\gamma \theta \frac m 2.
\tag{33}
$$
В данном случае для вычисления размаха пульсаций потребуется определить длительность пассивной фазы полутакта \(\theta\).
После завершения одного полутакта (когда напряжение источника достигает положительного или отрицательного амплитудного значения), начинается следующий. В начале полутакта все диоды умножителя закрыты, обмен зарядами между конденсаторами отсутствует, напряжение конденсаторов с нечётными номерами сохраняется неизменным, напряжение конденсаторов с чётными номерами линейно падает в результате разряда током нагрузки. В некоторый момент, когда мгновенное напряжение источника по модулю достигает определённого уровня, один из диодов умножителя открывается и начинается активная фаза полутакта, в процессе которой происходит передача зарядов между конденсаторами. Как было установлено ранее, первым открывается диод данного направления с наибольшим номером (наиболее удалённый от точки подключения источника). Для полутакта, который в нашем рассмотрении является вторым, это будет диод Dm. Он откроется в момент, когда разность потенциалов между его электродами обратится в 0:
$$
u(t)+U^*_1+U^*_3+\ldots+U^*_{m-1}-U^*_2-U^*_4-\ldots-U^*_m=0,
\tag{34}
$$
где звёздочками обозначены напряжения на конденсаторах в момент, когда диод открывается. Эти напряжения равны для конденсаторов с нечётными номерами напряжениям на начало полутакта, для конденсаторов с чётными номерами они будут меньше значений в начале полутакта на величину падения в результате разряда током нагрузки в течение пассивной фазы полутакта:
$$
U^*_j=U'_j, j=1, 3, \ldots, m-1, \\
U^*_i=U'_i-\gamma \theta, i=2, 4, \ldots, m,
$$
тогда (34) примет вид
$$
u(t)+U'_1+U'_3+\ldots+U'_{m-1}-U'_2-U'_4-\ldots-U'_m-\frac m 2 \theta \gamma=0
$$
(так как количество конденсаторов с чётными номерами составляет m/2).
Перегруппируем слагаемые следующим образом:
$$
u(t)+U'_1-(U'_2-U'_3)-(U'_4-U'_5)-\ldots-(U'_{m-2}-U'_{m-1})-U'_m-\frac m 2 \theta \gamma=0.
\tag{35}
$$
В соответствии с (13), величины со штрихом выражаются через величины на начало такта следующим образом:
$$
\begin{cases}
U'_1=U_a, \\
U'_m=U_m-\Delta U, \\
U'_{j-1}=\frac 1 2 (U_{j-1}+U_j-\Delta U)-\frac 1 2 \gamma \frac{j-1}2 \theta_1, \\
U'_j=\frac 1 2 (U_{j-1}+U_j-\Delta U)+\frac 1 2 \gamma \frac{j-1}2 \theta_1, \\
j=3, 5, ..., m-1,
\end{cases}
$$
откуда следует, что
$$
U'_{j-1}-U'_j=-\gamma \frac{j-1}2 \theta_1, \\
j=3, 5, \ldots, m-1,
$$
тогда сумма в (35) может быть вычислена как
$$
-(U'_2-U'_3)-(U'_4-U'_5)-\ldots-(U'_{m-2}-U'_{m-1})=-\sum_j(U'_{j-1}-U'_j)=\\
=\gamma \theta_1 \sum_j \frac{j-1}2=\gamma \theta_1 \sum_{k=1}^{(m-2)/2}k=\\
=\gamma \theta_1 \frac{m-2}2 \frac{1+\frac{m-2}2}2=\\
=\gamma \theta_1 \frac{m-2}2 \frac m 4=\gamma \theta_1 \frac{m^2-2m}8
$$
и (35) примет вид
$$
u(t)+U'_1+\gamma \theta_1 \frac{m^2-2m}8-U'_m-\frac m 2 \gamma \theta=0.
$$
Подставляем сюда значения для U'1 и U'm:
$$
u(t)+U_a+\gamma \theta_1 \frac{m^2-2m}8-U_m+\Delta U-\frac m 2 \gamma \theta=0.
$$
Далее, из (26) нам известно, что
$$
U_m=2U_a+\Delta U \left( -\frac{m^2}2-\frac m 2+1 \right),
$$
тогда
$$
u(t)+U_a+\gamma \theta_1 \frac{m^2-2m}8-2U_a+\Delta U \frac{m^2}2+\Delta U \frac m 2-\Delta U+\Delta U-\frac m 2 \gamma \theta=0,
$$
$$
u(t)-U_a+\gamma \theta_1 \frac{m^2-2m}8+\Delta U \frac{m^2}2+\Delta U \frac m 2-\frac m 2 \gamma \theta=0.
$$
Выразим \(\theta_1\) через \(\theta\) и подставим в последнее выражение
$$
\theta_1=\left( \frac T 2 -\theta \right)/(m/2)=\left( \frac T 2 -\theta \right) \frac 2 m, \\
\gamma \theta_1 \frac{m^2-2m}8=\gamma\left( \frac T 2-\theta \right)\frac 2 m \frac{m^2-2m}8=\\
=\gamma\left( \frac T 2-\theta \right) \frac{m-2}4=\gamma \frac T 2 \frac{m-2}4-\gamma \theta \frac{m-2}4=\\
=\Delta U \frac{m-2}4-\gamma \theta \frac{m-2}4=\Delta U\frac m 4-\Delta U\frac 1 2-\gamma \theta \frac m 4+\gamma\theta\frac 1 2.
$$
Считая питающее напряжение гармоническим и с учётом того, что на протяжении второго полутакта мгновенное значение питающего напряжения изменяется от -Ua до +Ua, выбирая за начало отсчёта времени начало второго полутакта, получаем что \(u(t)=-U_a\cos\omega t, \omega=2\pi/T\) и в момент перехода в активную фазу
$$
u(\theta)=-U_a\cos\omega\theta.
$$
Уравнение приобретает вид
$$
-U_a(\cos\omega\theta+1)+\gamma\theta\left(-\frac{3m}4+\frac 1 2\right)+\Delta U\left(\frac{3m}4-\frac 1 2+\frac{m^2}2\right)=0
$$
или
$$
-U_a\left(\cos\frac{2\pi\theta}T+1\right)+\gamma\theta\left(-\frac{3m}4+\frac 1 2\right)+\gamma \frac T 2 \left(\frac{3m}4-\frac 1 2+\frac{m^2}2\right)=0.
\tag{36}
$$
Уравнение не решается в общем виде относительно \(\theta\), может быть решено только численными методами (решение ищем на интервале 0..T/2). Также можно решить уравнение приближённо, при условии, что результат близок к значению T/2 (слабо нагруженный умножитель)
$$
\gamma \theta \approx \gamma \frac T 2,
$$
преобладающим становится слагаемое \(\Delta U m^2/2\) и уравнение (36) приобретает вид
$$
-U_a(\cos\omega\theta+1)+\Delta U \frac{m^2}2 \approx 0,
$$
откуда
$$
\cos\omega\theta \approx \frac{\Delta U}{U_a}\frac{m^2}2-1,
$$
$$
\theta \approx \frac 1 {\omega} \arccos\left( \frac{\Delta U}{U_a}\frac{m^2}2-1 \right).
\tag{37}
$$
Например, если умножитель является восьмикратным (m=8), Ua=100 В, F=50 Гц, ΔU=1 В (I=1 мА, C=10 мкФ), то даваемое формулой значение составит 7.38 мс. Численное решение уравнения (36) даст в этом случае значение 7.32 мс.
Можно предложить приближение и без тригонометрических функций. Так, если величина θ близка к T/2, то \(\omega \theta\) будет близко к π и может быть представлено как
$$
\omega \theta=\pi+\Delta x,
$$
где
$$
\Delta x=-\omega(T/2-\theta) \; -
$$
малая величина. Разложим функцию \(\cos(\pi+\Delta x)\) в ряд, ограничившись первыми членами разложения:
$$
\cos(\pi+\Delta x) \approx -1+\frac{\Delta x^2}2
$$
или в нашем случае
$$
\cos \omega \theta \approx -1+\frac{\omega^2 (T/2-\theta)^2}2.
$$
Нам известно, что
$$
\cos\omega\theta \approx \frac{\Delta U}{U_a}\frac{m^2}2-1,
$$
тогда
$$
-1+\frac{\omega^2 (T/2-\theta)^2}2 \approx \frac{\Delta U}{U_a}\frac{m^2}2-1, \\
(T/2-\theta)^2 \approx \frac{\Delta U m^2}{\omega^2 U_a}, \\
\theta \approx \frac T 2 - \frac m{\omega} \sqrt{\frac{\Delta U}{U_a}}.
$$
Для приведённого выше примера формула даёт значение 7.45 мс, что по точности уступает приближению, даваемому формулой (37), но ещё годится для грубых оценок.
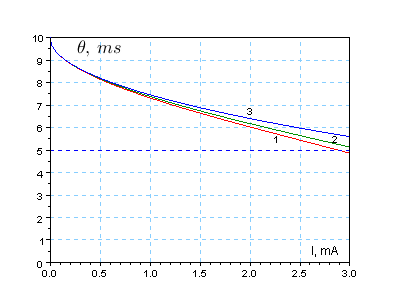
Рис. %img:i3
На рис. %img:i3 изображены графики зависимости длительности пассивной фазы полутакта от тока нагрузки для данного умножителя (m=8, Ua=100 В, F=50 Гц, C=10 мкФ) при изменении тока нагрузки от 0 до 3 мА. Верхнему пределу изменения тока соответствует падение напряжения под нагрузкой около 30% от номинального значения выходного напряжения, таким образом, рассматриваемый диапазон токов охватывает все практически значимые режимы работы умножителя (нецелесообразно использовать умножитель при больших, чем эти значения падениях напряжения). Линия 1 (красного цвета) построена по точным значениям, получаемым путём решения уравнения (36). Линия 2 (зелёного цвета) соответствует приближённой формуле (37). Линия 3 (синего цвета) построена по последней приближённой формуле, которая, как видим, уступает по точности формуле (37). На графике значение 10 мс по оси θ соответствует половине периода (T/2), а значение 5 мс (уровень обозначен на графике синим пунктиром) соответствует четверти периода (T/4). Как мы и предполагали, при нулевом токе, θ обращается в T/2. А при больших токах нагрузки длительность пассивной фазы становится даже меньше, чем четверть периода, это означает, что переключения диодов начинаются ещё до пересечения величиной u(t) нулевого уровня.
На следующем рисунке (рис. %img:i4) изображены графики относительных погрешностей, даваемых приближёнными формулами. Пунктиром на рисунке обозначены уровни погрешности 5% и 10%. Видим, что формула (37) достаточно точна в рассматриваемом диапазоне токов нагрузки, где её погрешность практически всюду менее 5% (зелёная линия). Вторая приближённая формула может применяться только при весьма малых токах (синяя линия).
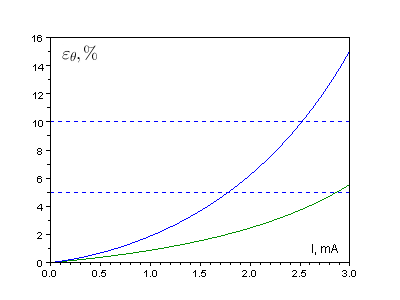
Рис. %img:i4
Зная длительность пассивной фазы, можем вычислить время пребывания отдельного диода в открытом состоянии:
$$
\theta_1=(T/2-\theta)/(m/2)
$$
и построить график зависимости этой величины от тока нагрузки (рис. %img:i5). Видим, что данная величина, как и предполагалось, равна нулю в идеальном умножителе при отсутствии нагрузки. На начальном участке зависимости можно наблюдать очень высокую скорость роста величины, т.е. даже при малых токах нагрузки, влияние времени переключения на работу схемы становится ощутимым.
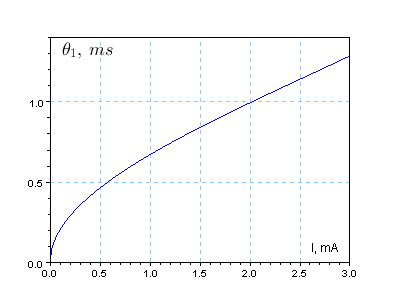
Рис. %img:i5
Оценим амплитуду импульсов тока через крайние диоды умножителя: Dm и D1. В каждый момент времени может быть открытым не более чем один диод. Переходя в открытое состояние, диод создаёт замкнутый контур из конденсаторов и источника питания. В соответствии со свойствами конденсатора, ток через конденсатор C, подключённый к источнику u(t),
$$
I_C=C\frac{du(t)}{dt}.
$$
Когда открывается диод Dm, создаётся контур из источника и m последовательно соединённых конденсаторов, каждый из которых имеет ёмкость C, значит, их общая ёмкость равна C/m. Диод Dm открывается на втором полутакте, через промежуток времени θ от начала полутакта. Как было установлено в предыдущем пункте, если за начало отсчёта времени принять начало второго полутакта, то мгновенное напряжение источника
$$
u(t)=-U_a\cos\omega t,
$$
а ток через конденсаторы (общей ёмкостью C/m) при открытом диоде Dm равен
$$
I_{Dm}=\frac{U_a \omega C}m \sin\omega t
$$
и наибольшего значения достигает в момент, когда диод открывается:
$$
I_{Dm}=\frac{U_a \omega C}m \sin\omega \theta.
$$
В качестве θ возьмём приближённое значение, даваемое формулой (37), а также учтём, что
$$
\sin\arccos x=\sqrt{1-\cos^2 \arccos x}=\sqrt{1-x^2},
$$
тогда
$$
I_{Dm} \approx \frac{U_a \omega C}m \sqrt{1-\left(\frac{m^2 \Delta U}{2U_a}-1\right)^2}= \\
=\frac{U_a \omega C}m \sqrt{1-\left(\frac{m^2 \Delta U}{2U_a}\right)^2+\frac{m^2 \Delta U}{U_a}-1}= \\
=U_a \omega C \sqrt{\frac{\Delta U}{U_a}-\left(\frac{\Delta U m}{2U_a}\right)^2}.
$$
Считая второе слагаемое под знаком корня малым по сравнению с первым ввиду малости \(\Delta U\) по сравнению с Ua, можем записать
$$
I_{Dm} \approx U_a \omega C \sqrt{\frac{\Delta U}{U_a}}.
\tag{38}
$$
Выражая входящие в формулу величины через базовые
$$
\omega=2\pi F, \\
\Delta U=\frac I{2FC},
$$
получим
$$
I_{Dm} \approx \sqrt{2{\pi}^2 FCU_a I},
\tag{39}
$$
здесь I, как и ранее, потребляемый нагрузкой умножителя ток.
Что касается диода D1, то он открывается за время \(\theta_1\) до окончания первого полутакта и закрывается в момент завершения этого полутакта, данный диод подключает к источнику единственный конденсатор ёмкостью C. Максимальное значение тока также достигается в начальный момент (затем, к концу полутакта ток постепенно падает до 0) и может быть вычислено как
$$
I_{D1}=U_a \omega C \sin \omega \theta_1.
$$
Если \(\theta_1\) мало по сравнению с длительностью периода, то
$$
\sin \omega \theta_1 \approx \omega \theta_1=\omega\frac{2(T/2-\theta)}m \approx \\
\approx \omega \frac{2\frac m{\omega}\sqrt{\frac{\Delta U}{U_a}}}m=2\sqrt{\frac{\Delta U}{U_a}},
$$
тогда
$$
I_{D1} \approx 2 U_a \omega C \sqrt{\frac{\Delta U}{U_a}}
$$
или
$$
I_{D1} \approx \sqrt{8{\pi}^2 FCU_a I},
\tag{40}
$$
оценочное значение максимального тока через первый диод получилось вдвое больше чем для диода Dm.
Это, в основном, соответствует действительности. В установившемся режиме максимальное значение импульсного тока через последний диод может быть чуть больше значения, даваемого формулой (39), а значение тока в максимуме через первый диод обычно чуть меньше, чем даёт формула (40). Для промежуточных диодов импульсный ток принимает промежуточные значения.
Среднее значение тока через диоды равно току нагрузки.
Понятно, что формулы (39), (40) неприменимы к переходному процессу, во время которого, если не принять специальных мер, ток через диоды (особенно в начале схемы) может во много раз превышать значения в установившемся режиме.
author: hamper; date: 2017-01-29; modified: 2017-01-31





