Рис. %img:a1
| [Home] | [Donate!] [Контакты] |
Возможно ли это?
Почему такое возможно?
До какой степени это возможно?
Сигнал с самой большой амплитудой гармоники
Выводы
Амплитуда, как известно - величина наибольшего отклонения мгновенного значения сигнала от среднего значения. Это понятие используют обычно применительно к периодическим сигналам или к "почти" периодическим. В первом случае амплитуда является величиной постоянной, а во втором может изменяться со временем, но должна делать это достаточно медленно, на протяжении большого количества периодов сигнала, иначе говорить об амплитуде становится бессмысленно.
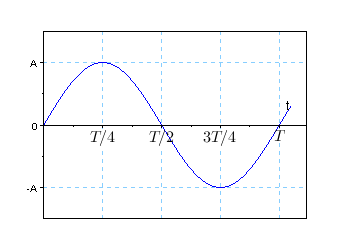
На следующем рисунке A - амплитуда синусоидального сигнала.
Сигнал может быть несимметричным, на следующем рисунке \( A_+ \neq A_- \)
Периодический сигнал можно представить в виде суммы гармонических составляющих с частотами, кратными частоте сигнала, т.е. разложить в ряд Фурье. Амплитуды гармоник зависят от амплитуды и формы сигнала.
Вопрос в том, может ли быть амплитуда сигнала меньше, чем амплитуда какой-то из гармоник сигнала?
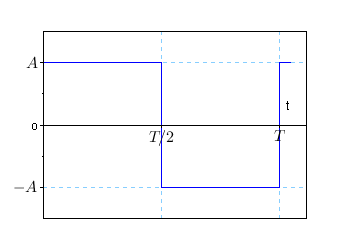
Рис. %img:m. Меандр - частный случай колебаний прямоугольной формы
Вопрос, впрочем, глупый. Конечно, амплитуда сигнала может быть меньше амплитуды одной из его гармоник! Или, что то же самое, амплитуда одной из гармоник сигнала может превышать амплитуду самого сигнала! (Правда не намного, но об этом позже). Может и это не редкое явление. Классический пример - у меандра с амплитудой 1 первая гармоника имеет амплитуду \( 4/ \pi \gt 1 \). Амплитуда первой гармоники превышает амплитуду меандра примерно на 27%: \( 4/\pi \approx 1.27 \). Другой, важный с практической точки зрения пример: в мощных резонансных усилителях (например, в усилителях мощности радиопередающих устройств) может использоваться 3-я гармоника сигнала для уменьшения амплитуды напряжения на активном элементе усилителя и облегчения тем самым его режима работы.
Коль скоро мы убедились в том, что амплитуда гармоники может быть больше амплитуды сигнала, было бы интересно ответить и на другие вопросы, вроде следующих: а как такое вообще возможно; и насколько сильно может амплитуда гармоники превышать амплитуду сигнала; может ли быть больше одной такой гармоники?
Принципиально возможность того, что сигнал будет иметь амплитуду, меньшую чем амплитуды гармоник можно объяснить следующим образом. С одной стороны, складывая несколько составляющих, имеющих разные частоты, мы получаем сигнал, средняя мощность которого равна сумме средних мощностей составляющих и, стало быть, мощность сигнала больше мощности составляющих. С другой стороны, мощность сигнала определяет действующее значение сигнала*, а не амплитуду. При определённых соотношениях между гармониками они будут гасить пиковые значения друг друга.
* Действующее значение амплитуды характеризует среднюю мощность сигнала. Например, действующее напряжение источника - это такое постоянное напряжение, которое бы на чисто активной нагрузке рассеивало такую же мощность, что и данный источник на той же нагрузке. Действующее напряжение для периодического сигнала с периодом T и мгновенным напряжением u(t): $$ U_e=\sqrt {\frac 1 T \int \limits_0^T u^2dt}. $$
То, каким образом происходит уменьшение амплитуды сигнала по сравнению с амплитудой гармоники, лучше всего демонстрирует простейший пример, когда сигнал состоит всего из двух гармоник с отличающимися в 3 раза частотами: $$ u(t)=\sin \omega t + a \sin 3 \omega t. $$ Амплитуду первой гармоники для простоты принимаем равной 1, амплитуду следующей принимаем равной a.
На рисунках изображены обе составляющие сигнала по отдельности и результат их суммирования.
Как видим, за счёт высокочастотной составляющей с меньшей амплитудой, в области пиков низкочастотной составляющей с большей амплитудой появляются провалы, которые уменьшают амплитуду результирующего сигнала (при этом импульсы становятся более широкими в области максимальных отклонений, за счёт чего увеличивается действующее значение).
Найдём амплитуду полученного сигнала. В силу периодичности и симметричности функции u(t), достаточно рассмотреть функцию на интервале \( 0 \lt \omega t \lt \pi/2 \) и на нём найти максимум функции.
Точку максимума найдём из условия: $$ u'(t)=0,\\ \omega \cos \omega t + 3 a \omega \cos 3 \omega t=0,\\ \cos \omega t + 3 a \cos 3 \omega t=0. $$ Косинус тройного угла не входит в число обязательных формул, которыми стоит забивать голову, так что выразим его с помощью формулы косинуса суммы: $$ \cos 3\omega t=\cos(\omega t+2\omega t)= \cos \omega t \cos 2\omega t-\sin \omega t \sin 2\omega t. $$ С учётом того, что $$ \cos 2\omega t=1-2\sin^2 \omega t,\\ \sin 2\omega t=2\sin \omega t \cos \omega t, $$ получаем для косинуса тройного угла выражение $$ \cos 3\omega t=\cos \omega t(1-2\sin^2 \omega t)-2\sin^2 \omega t \cos \omega t,\\ \cos 3\omega t=\cos \omega t(1-4\sin^2 \omega t). $$ Тогда уравнение приобретает вид: $$ \cos \omega t + 3a \cos \omega t(1-4\sin^2 \omega t)=0. $$ На рассматриваемом интервале \( \cos \omega t \neq 0 \), поэтому данное уравнение равносильно уравнению $$ 1+3a-12a\sin^2 \omega t=0,\\ \sin^2 \omega t=\frac {1+3a} {12a}. $$ Теперь воспользуемся тригонометрической формулой для квадрата синуса \( \sin^2 \alpha=(1-\cos 2\alpha)/2 \), получим $$ \frac {1-\cos 2\omega t} 2=\frac {1+3a} {12a},\\ 1-\cos 2\omega t=\frac {1+3a} {6a},\\ \cos 2\omega t=1-\frac {1+3a} {6a}=\frac {6a-1-3a} {6a}=\frac {3a-1} {6a}. $$ Чтобы прийти к какому нибудь числовому значению и посмотреть, что же в итоге получилось, положим a=1/3, тогда (3a-1)/(6a)=0 и $$ \cos 2\omega t=0. $$ Это уравнение на рассматриваемом интервале имеет единственное решение $$ 2 \omega t=\frac {\pi} 2, \\ \omega t=\frac {\pi} 4. $$ Вычисляя значение функции u(t) в найденной точке, определяем амплитуду сигнала в случае, когда a=1/3: $$ A=\sin \frac {\pi} 4 + \frac 1 3 \sin \frac {3\pi} 4= \frac {\sqrt 2} 2 + \frac 1 3 \frac {\sqrt 2} 2= \frac {3\sqrt 2+\sqrt 2} 6= \frac {4\sqrt 2} 6= \frac {2\sqrt 2} 3= \frac {\sqrt 8} {\sqrt 9}= \sqrt {\frac 8 9}. $$ Получили, что амплитуда сигнала $$ A=\sqrt \frac 8 9 \lt 1, $$ так как 8/9<1. Не забываем также, что амплитуду первой гармоники мы приняли равной 1 (смотрите выражение для функции u(t)).
Итак, нам удалось сконструировать сигнал, который содержит гармонику с амплитудой большей, чем амплитуда самого сигнала. Правда в данном случае превышение небольшое, \( A=\sqrt {8/9} \approx 0.94 \), так что амплитуда наибольшей гармоники превышает амплитуду сигнала всего лишь на величину порядка 6%, но тут важен сам факт.
Полученный результат - не предел. В нашем примере, как показывает численный анализ, минимум амплитуды сигнала u(t) достигается при значении параметра \( a \approx 0.17 \), и его значение составляет около 0.866, что означает превышение амплитуды первой гармоники по сравнению с амплитудой сигнала примерно на 15%.
График зависимости амплитуды U функции u(t) от параметра a - амплитуды гармоники с тройной частотой:
Но ведь существуют и другие классы функций, для которых эффект может проявляться в большей степени. Допустим к рассмотренному сигналу u(t) можно добавить ещё одну гармонику с частотой в 5 раз больше основной, которая будет создавать "провалы" в области пиковых значений и тем самым ещё немного уменьшать амплитуду сигнала. Затем такую операцию можно повторять ещё и ещё, каждый раз добавляя новую гармонику, которая будет компенсировать пиковые значения сигнала, сконструированного на предыдущем этапе.
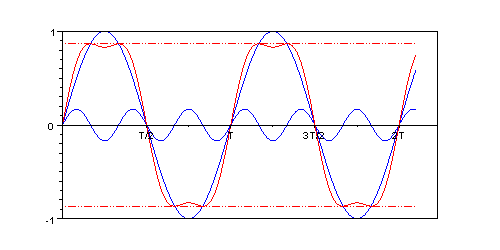
Рис. %img:i1. Шаг 1. \( u(t)=\sin \omega t +0.17\sin 3\omega t \), амплитуда \( \approx 0.866 \)
Каков же предел, до которого можно уменьшать амплитуду сигнала? На сколько амплитуда гармоники сигнала может превышать амплитуду сигнала?
Чтобы охватить сразу все возможные варианты сигналов, необходим какой-то более общий подход. В таких случаях бывает продуктивным рассмотрение явлений с энергетической точки зрения.
Пусть некоторый сигнал задан функцией u(t)=u1(t)+u2(t)+... Здесь u1(t), u2(t) - гармонические составляющие сигнала. Так как все составляющие имеют разную частоту, то средняя мощность сигнала равна сумме средних мощностей составляющих гармоник (имеется в виду мощность, рассеиваемая на чисто активном сопротивлении, подключённом к источнику сигнала). Мощность пропорциональна квадрату действующего напряжения. Поэтому для действующих напряжений будет справедливо равенство: $$ U_e^2=U1_e^2+U2_e^2+\ldots \tag{1} $$ Далее, как известно, действующее значение сигнала никогда не превышает амплитуды. Если не известно, то это легко показать. Для любого периодического сигнала (считаем, что постоянная составляющая отсутствует, т.е. среднее значение равно 0) по определению амплитуды в любой момент времени выполняется неравенство $$ |u(t)| \le U_a, $$ где u(t) - мгновенное значение; Ua - амплитуда. Значит, $$ u^2 \le U_a^2, $$ а значит неравенство будет выполняться и для средних за период значений величин: $$ \frac 1 T \int \limits_0^T u^2 dt \le \frac 1 T \int \limits_0^T U_a^2 dt. $$ Но выражение слева - это квадрат действующего значения, а выражение справа просто равно квадрату амплитуды, так как Ua=const: $$ U_e^2 \le U_a^2, $$ а значит и $$ U_e \le U_a. $$
Так как квадрат действующего значения для гармонического сигнала равен половине квадрата амплитуды этого сигнала, то равенство (1) можно записать в следующем виде: $$ U_e^2=\frac {U1_a^2} 2 + \frac {U2_a^2} 2 + \ldots \tag{2} $$ Как мы установили, \( U_a^2 \ge U_e^2 \), поэтому с учётом (2) получаем: $$ U_a^2 \ge \frac {U1_a^2} 2 + \frac {U2_a^2} 2 + \ldots \tag{3} $$
Из неравенства (3) следует, что не более чем одна гармоника может иметь амплитуду больше амплитуды сигнала.
Предположим что это не так и есть хотя бы две такие гармоники. Переупорядочим правую часть (3) так, чтобы первые два слагаемых соответствовали гармоникам с наибольшей амплитудой. Сумму всех остальных слагаемых обозначим R, \( R \ge 0 \) как сумма квадратов действительных величин. $$ U_a^2 \ge \frac {U1_a^2} 2 + \frac {U2_a^2} 2 + R, $$ и в соответствии с нашим предположением $$ \left\{ \begin{matrix} U1_a \gt U_a, \\ U2_a \gt U_a; \end{matrix} \right. \\ \left\{ \begin{matrix} U1_a^2 \gt U_a^2, \\ U2_a^2 \gt U_a^2; \end{matrix} \right. \\ U1_a^2+U2_a^2 \gt 2U_a^2, \\ U_a^2 \lt \frac {U1_a^2} 2 + \frac {U2_a^2} 2. $$ Тогда тем более $$ U_a^2 \lt \frac {U1_a^2} 2 + \frac {U2_a^2} 2 + R, $$ но это противоречит условию (3).
Сделанное нами предположение о возможности существования двух гармоник в сигнале с амплитудами, большими амплитуды сигнала привело к противоречию. Стало быть, предположение неверно и не более одной гармоники в сигнале может иметь амплитуду, большую амплитуды самого сигнала.
Конечно это не значит, что в любом сигнале есть такая гармоника. Очень часто гармоники ведут себя прилично и не "вылезают" за амплитуду сигнала.
Условие (3) даёт нам важную информацию о нижней границе амплитуды сигнала. Эта амплитуда ни при каких условиях не может быть меньше следующей величины: $$ U1_a \ge \sqrt {\frac {U1_a^2} 2 + \frac {U2_a^2} 2 + \ldots}. $$ Минимальный нижний предел амплитуды сигнала мы получим, когда сумма квадратов амплитуд всех гармоник, кроме гармоники с наибольшей амплитудой, стремится к 0: $$ \sum_i \frac {{Ui_a}^2} 2 \rightarrow 0, $$ в этом случае $$ U_a \ge \frac {U1_a} {\sqrt 2}, $$ а если амплитуду наибольшей гармоники принять равной 1, то \( U_a \ge 1/\sqrt 2 \approx 0.707 \). Амплитуда гармоники теоретически не может более чем на 42% превышать амплитуду сигнала! В действительности это значение меньше, так как понятно, что все гармоники кроме основной не могут быть равны 0, иначе мы просто получим гармонический сигнал, амплитуда которого, очевидно, равна амплитуде единственной составляющей. Но если будут присутствовать высшие гармоники, уменьшающие пиковые значения наибольшей гармоники, то они будут сдвигать найденную нами границу.
Вернёмся опять к случаю, когда сигнал содержит всего две гармонические составляющие. Как было показано, одновременно две гармоники не могут иметь амплитуды больше амплитуды сигнала. Поэтому, если амплитуда одной гармоники будет больше амплитуды сигнала, то амплитуда другой - меньше амплитуды сигнала (т.е. в нашем случае равными они также не могут быть). Будем считать что гармоника u1 имеет наибольшую амплитуду, мы можем принять её амплитуду равной 1 (это лишь вопрос масштабирования). $$ u(t)=u1(t)+u2(t), \\ U1_a=1, U2_a \lt 1, \\ $$ $$ U_a \ge \sqrt {\frac 1 2 + \frac {U2_a^2} 2}. \tag{4} $$ С другой стороны, в моменты, когда гармоника u1 достигает наибольшего значения, значение функции u(t) не может быть меньше, чем \( U1_a-U2_a=1-U2_a \) и то, при условии, что u2(t) достигает наименьшего значения в моменты, когда u1(t) имеет наибольшее значение и наоборот, значит для амплитуды сигнала мы можем записать следующее неравенство: $$ U_a \ge 1-U2_a. \tag{5} $$ Условия (4) и (5) должны выполняться одновременно. Выражение в правой части (4) растёт с ростом U2a, а выражение в правой части (5) убывает. Поэтому при малых U2a ограничивающим условием является (5), а при больших - (4). Условия (4), (5) можно объединить в одно следующим образом: $$ U_a \ge max \left(\sqrt {\frac 1 2 + \frac {U2_a^2} 2}, 1-U2_a \right). \tag{6} $$ Оба ограничения "встречаются" в некоторой точке U2a0, где достигается наименьшее значение выражения в правой части (6). Эту точку найдём из уравнения $$ \sqrt {\frac 1 2 + \frac {U2_{a0}^2} 2}=1-U2_{a0}, \\ \frac 1 2 + \frac {U2_{a0}^2} 2=1-2U2_{a0}+U2_{a0}^2, \\ U2_{a0}^2-4U2_{a0}+1=0. $$ Полученное квадратное уравнение имеет два решения: \( 2 \pm \sqrt 3 \), нас интересует только решение, меньшее 1. Этим решением является $$ U2_{a0}=2-\sqrt 3. $$ Тогда $$ U_a \ge 1-U_{2a}, \\ U_a \ge 1-2+\sqrt 3, \\ U_a \ge \sqrt 3-1 \approx 0.732. $$ Это более строгое ограничение, чем полученное для случая произвольного количества составляющих условие \(U_a \ge 1\sqrt 2 \), так как \( \sqrt 3 -1 \gt 1/\sqrt 2 \). Впрочем не намного.
Энергетический подход позволил определить границу для наибольшего значения амплитуды гармоники, т.е. теперь мы точно знаем, какую величину амплитуда гармоники превысить не может. А хотелось бы знать, какое максимальное значение она может иметь. Рассмотрим разложение периодического сигнала u(t) с периодом T в ряд Фурье в следующей форме: $$ u(t)=\frac {a_0} 2 + a_1\sin \left( \frac {2\pi} T t + \phi_1 \right) + u_a\sin \left( 2\frac {2\pi} T t + \phi_2 \right) + \ldots, \\ a_k=\frac 2 T \int \limits_0^T u(t) \sin \left( \frac {2\pi k t} T + \phi_k \right) dt. $$ Здесь ak - амплитуда гармоники k, а \( \phi_k \) - фаза. Будем считать, что наибольшую амплитуду имеет первая гармоника. Так как нас не интересует фаза сигнала (которая не влияет ни на форму сигнала, ни на амплитуды гармоник), а интересует только амплитудный спектр то выберем точку начала отсчёта времени так, чтобы \( \phi_1=0 \), тогда амплитуда первой гармоники равна: $$ a_1=\frac 2 T \int \limits_0^T u(t) \sin \frac {2\pi t} T dt. $$ Задача состоит в том, чтобы подобрать функцию u(t) заданной амплитуды, которая обеспечит наибольшее значение a1. Будем считать функцию кусочно-непрерывной, амплитуду u(t) будем считать не превышающей 1 (т.е. выберем соответствующий масштаб величин).
Нетрудно заметить, что u(t) следует искать среди функций, для которых в любой точке выполняется условие \( u(t) \sin \frac {2\pi t} T \ge 0 \), т.е. указанное произведение не должно менять знака, а значит знаки u(t) и \( \sin \frac {2\pi t} T \) должны совпадать в любой момент времени.
Обосновать это требование можно, например так. Предположим, что u1(t) - искомая функция (кусочно-непрерывная функция с амплитудой 1 и периодом T, амплитуда первой гармоники a1 которой имеет наибольшее среди всех возможных функций значение). И пусть есть точка t0, в которой \( u(t_0) \sin \frac {2\pi t_0} T \lt 0 \). Синус является непрерывной функцией, u(t) - кусочно-непрерывной, поэтому их произведение является кусочно-непрерывной функцией и можно найти отрезок [t1, t2] в окрестностях точки t0 на котором \( \left. u(t) \sin \frac {2\pi t} T \lt 0 \right|_{t \in [t_1, t_2]} \).
Амплитуду первой гармоники для функции u1 запишем в виде: $$ a_1(u1)=\frac 2 T \int \limits_0^{t_1} u1(t) \sin \frac {2\pi t} T dt+ \frac 2 T \int \limits_{t_1}^{t_2} u1(t) \sin \frac {2\pi t} T dt+ \frac 2 T \int \limits_{t_2}^T u1(t) \sin \frac {2\pi t} T dt. $$ Обозначим слагаемые в правой части выражения как I1, I2, I3, тогда \( a_1=I_1+I_2+I_3 \), причём I2<0, так как подынтегральное выражение на всём отрезке интегрирования отрицательно.
Теперь рассмотрим функцию u2(t), которая всюду равна u1(t), кроме отрезка [t1, t2], где u2(t)=-u1(t): $$ u2(t)=\left\{ \begin{matrix} u1(t), t \notin [t_1+nT, t_2+nT], \\ -u1(t), t \in [t_1+nT, t_2+nT], \end{matrix} \right. $$ Функция u2(t) будет также иметь период T и амплитуду, не превышающую 1. При этом амплитуда её первой гармоники равна $$ a_1(u2)=\frac 2 T \int \limits_0^{t_1} u2(t) \sin \frac {2\pi t} T dt+ \frac 2 T \int \limits_{t_1}^{t_2} u2(t) \sin \frac {2\pi t} T dt+ \frac 2 T \int \limits_{t_2}^T u2(t) \sin \frac {2\pi t} T dt=\\ =\frac 2 T \int \limits_0^{t_1} u1(t) \sin \frac {2\pi t} T dt- \frac 2 T \int \limits_{t_1}^{t_2} u1(t) \sin \frac {2\pi t} T dt+ \frac 2 T \int \limits_{t_2}^T u1(t) \sin \frac {2\pi t} T dt=\\ =I_1-I_2+I_3=a_1(u1)-2I_2,\\ a_1(u1) \lt a_1(u2), $$ так как I2<0. Но это противоречит предположению о том, что функция u1(t) имеет наибольшую первую гармонику, значит предположение неверно и функция с наибольшей первой гармоникой среди всех кусочно-непрерывных функций с периодом T и амплитудой, не превышающей 1 должна иметь в любой точке такой же знак, что и выражение \( \sin \frac {2\pi t} T \).
Искомая функция u(t), таким образом, будет принимать положительные значения в первую половину периода и отрицательные во вторую. Амплитуду первой гармоники можно записать в виде $$ a_1=\frac 2 T \int \limits_0^{T/2} u(t) \sin \frac {2\pi t} T dt+ \frac 2 T \int \limits_{T/2}^T u(t) \sin \frac {2\pi t} T dt. $$ Оба интеграла положительны, так как подынтегральные выражения положительны. Каждое из двух слагаемых можно максимизировать независимо, наибольшее значение получим в том случае, когда каждое из них будет иметь наибольшее значение.
Сначала максимизируем первое слагаемое, которое определяется видом функции u(t) на отрезке [0, T/2]. Можно предположить, что его наибольшему значению будет соответствовать функция u(t)=1. Действительно, для любой другой функции y(t), которая не является константой 1, существует точка t0, в которой y(t0)<1 (значение функции не может быть большим 1, т.к. 1 - амплитуда). А значит мы сможем найти целый отрезок, где y(t)<1 и на этом отрезке $$ y(t) \sin \frac {2\pi t} T \lt 1 \cdot \sin \frac {2\pi t} T. \tag{7} $$ Амплитуда функции y(t) равна 1, поэтому на отрезке [0, T/2] \( y(t) \le 1 \) или \( y(t) \le u(t) \). Тогда \( y(t) \sin \frac {2\pi t} T \le u(t) \sin \frac {2\pi t} T \) на этом отрезке и в соответствии со свойствами определённых интегралов $$ \int \limits_0^{T/2} y(t) \sin \frac {2\pi t} T dt \le \int \limits_0^{T/2} u(t) \sin \frac {2\pi t} T dt, \\ \frac 2 T \int \limits_0^{T/2} y(t) \sin \frac {2\pi t} T dt \le \frac 2 T \int \limits_0^{T/2} u(t) \sin \frac {2\pi t} T dt. $$ Кроме того, как мы установили, есть целый отрезок внутри отрезка [0, T/2], где выполняется (7). Можно доказать, что в таком случае $$ \frac 2 T \int \limits_0^{T/2} y(t) \sin \frac {2\pi t} T dt \lt \frac 2 T \int \limits_0^{T/2} u(t) \sin \frac {2\pi t} T dt, \\ a_1(y) \lt a_1(u). $$ а значит u(t)=1 - искомая функция.
Аналогично получаем, что на втором полупериоде u(t)=-1. Получилось, что функция данной амплитуды, имеющая первую гармонику с наибольшей амплитудой - это меандр $$ u(t)=\left\{ \begin{matrix} 1, nT \le t \lt T/2+nT, \\ -1, T/2+nT \le t \lt (n+1)T. \end{matrix} \right. $$
Может ли иметь наибольшую амплитуду не первая гармоника сигнала? Для сигнала данной амплитуды с наибольшей по амплитуде гармоникой - нет. Для оптимального в этом смысле сигнала наибольшую амплитуду будет иметь первая гармоника. Если предположить что наибольшая амплитуда может быть у гармоники с номером k>1, повторяя рассуждения, аналогичные приведённым выше, получим меандр с частотой k/T. Он будет иметь период T/k и для него гармоника с частотой k/T окажется первой.
Для "неоптимальных" сигналов наибольшей может быть и не первая гармоника. Например, можно взять любой сигнал, амплитуда которого меньше, чем амплитуда первой гармоники и добавить достаточно маленькую составляющую с любой частотой, меньшей частоты первой гармоники. В новом сигнале добавленная гармоника станет первой и она не будет наибольшей. А амплитуда наибольшей гармоники по-прежнему будет превышать амплитуду сигнала, если добавленная составляющая достаточно мала. Даже если наибольшая гармоника не будет первой, она будет в значительной степени определять форму сигнала (так как все остальные гармоники будут иметь меньшую амплитуду) и сигнал получится сильно осциллирующим.
Итак, что удалось выяснить. Действительно, сигнал может содержать гармоники с амплитудами большими, чем амплитуда самого сигнала. Но в количестве не более одной! И превышение это не может быть большим, наибольшая амплитуда гармоники не может превышать амплитуду сигнала более чем в \( 4/\pi \) раз (примерно на 27%). Сигнал, который имеет гармонику с наибольшей амплитудой по сравнению с амплитудой самого сигнала - меандр.
На практике эти сведения можно использовать следующим образом. Если, например, на устройство воздействует сигнал помехи и удалось оценить амплитуду сигнала, но не известен его спектр, то для решения оценочных задач, можно смело считать, что по порядку величины амплитуда никакой из гармоник не превысит амплитуду сигнала.