| [Home] | [Donate!] [Контакты] |
Тригонометрические функции - это следующие, относящиеся к классу элементарных, функции:
| Обозначение | Название | Встречающиеся альтернативные обозначения |
|---|---|---|
| sin x | синус | |
| cos x | косинус | |
| tg x | тангенс | tan x |
| ctg x | котангенс | cot x, cotg x, ctn x |
| sec x | секанс | sc x |
| cosec x | косеканс | csc x, cosc x, csec x |
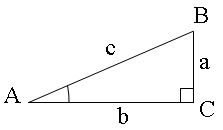
Определения для тригонометрических функций вводят, рассматривая соотношения сторон в прямоугольном треугольнике. Таким образом можно определить тригонометрические функции острых углов.

Синус острого угла треугольника - отношение противолежащего катета к гипотенузе, косинус - отношение прилежащего катета к гипотенузе, тангенс - отношение противолежащего катета к прилежащему и т.д. $$\sin A=a/c,$$ $$\cos A=b/c,$$ $$\operatorname{tg} A=a/b.$$
Другой, более общий подход, состоит в использовании единичной окружности для определения тригонометрических функций.
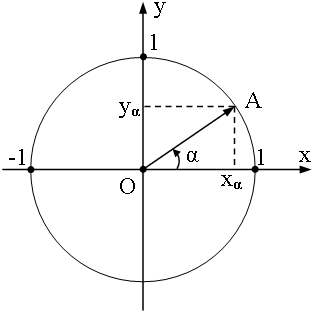
Пусть A - точка окружности с центром в начале прямоугольной системы координат O и радиусом равным единице; α - угол между осью абсцисс и вектором \( \vec {OA} \). Углы отсчитываются от положительного направления оси Ox, при отсчёте против часовой стрелки угол считается положительным, при отсчёте по часовой стрелке - отрицательным.
Если (xα, yα) - координаты точки A, то синус и косинус определяются следующим образом: $$\sin\alpha=y_\alpha; \\ \cos\alpha=x_\alpha.$$
Все остальные тригонометрические функции могут быть определены через синус и косинус: $$\operatorname{tg} \alpha=\frac{\sin\alpha}{\cos\alpha}, $$ $$\operatorname{ctg} \alpha=\frac{\cos\alpha}{\sin\alpha}, $$ $$\sec\alpha=\frac 1 {\cos\alpha}; $$ $$\operatorname{cosec} \alpha=\frac 1 {\sin\alpha}.$$
На практике обычно ограничиваются использованием функций sin, cos и tg. Остальные тригонометрические функции используются крайне редко, вместо этих функций сразу подставляют соответствующее им выражение.
| Название | Область определения | Множество значений | Чётность | Период |
|---|---|---|---|---|
| sin x | (−∞, +∞) | [−1, +1] | Н | 2 π |
| cos x | (−∞, +∞) | [−1, +1] | Ч | 2 π |
| tg x | (−∞, +∞) кроме точек π / 2 + π n* | (−∞, +∞) | Н | π |
| ctg x | (−∞, +∞) кроме точек π n | (−∞, +∞) | Н | π |
| sec x | (−∞, +∞) кроме точек π / 2 + π n | (−∞, -1]U[+1, +∞) | Ч | 2 π |
| cosec x | (−∞, +∞) кроме точек π n | (−∞, -1]U[+1, +∞) | Н | 2 π |
* В этой таблице n - любое целое.
Знак значения тригонометрической функции зависит от того, в какой четверти находится аргумент. На следующем рисунке показаны знаки по четвертям для sin x и cos x (верхний/нижний символ).

Формулами приведения называют формулы вида: $$\sin\left(\frac\pi 2\pm\alpha\right)=\cos\alpha, \\ \cos\left(\frac\pi 2\pm\alpha\right)=\mp\sin\alpha, \\ \sin(\pi\pm\alpha)=\mp\sin\alpha, \\ \cos(\pi\pm\alpha)=-\cos\alpha, \\ \ldots$$
Обычно используются не в явном виде как формулы, а в виде правила, позволяющего перейти от тригонометрической функции аргумента \( \pi/2\pm\alpha,\, \pi\pm\alpha,\, 3\pi/2\pm\alpha \) и т.д. к функции от \( \alpha \).
Правило следующее: 1) знак перед функцией справа будет таким же, что и у исходной функции от её аргумента, если считать \( \alpha \) острым (для определения знака функции можем посмотреть, в какой квадрант попадает аргумент); 2) если постоянное слагаемое кратно \( \pi \), функция остаётся той же, что в левой части, а если не кратно \( \pi \), но кратно \( \pi/2 \) - меняется на кофункцию (sin на cos и наоборот, tg на ctg и наоборот).
Формулы приведения позволяют тригонометрическую функцию любого аргумента выразить через значения тригонометрических функций аргумента, лежащего в первой четверти.
Соотношения между функциями одного аргумента. $$\sin^2\alpha+cos^2\alpha=1 \\ \operatorname{tg} \alpha=\frac{\sin\alpha}{\cos\alpha} \\ 1+\operatorname{tg} ^2\alpha=\frac 1 {\cos^2\alpha}$$
Функции суммы и разности двух аргументов.
Синус суммы: $$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$$ Синус разности: $$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$$ Косинус суммы: $$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$$ Косинус разности: $$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$$
Синус двойного угла: $$\sin 2\alpha=2\sin\alpha\cos\alpha$$ Косинус двойного угла: $$\cos 2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha$$
Суммы и разности тригонометрических функций.
Сумма синусов: $$\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta} 2 \cos\frac{\alpha-\beta} 2$$ Разность синусов: $$\sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta} 2 \sin\frac{\alpha-\beta} 2$$ Сумма косинусов: $$\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta} 2 \cos\frac{\alpha-\beta} 2$$ Разность косинусов: $$\cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta} 2 \sin\frac{\alpha-\beta} 2$$
Произведение тригонометрических функций.
Синус на синус: $$\sin\alpha\sin\beta=\frac{\cos(\alpha-\beta)-\cos(\alpha+\beta)} 2$$ Синус на косинус: $$\sin\alpha\cos\beta=\frac{\sin(\alpha-\beta)+\sin(\alpha+\beta)} 2$$ Косинус на косинус: $$\cos\alpha\cos\beta=\frac{\cos(\alpha-\beta)+\cos(\alpha+\beta)} 2$$
Квадраты тригонометрических функций.
Квадрат синуса: $$\sin^2\alpha=\frac{1-\cos 2\alpha} 2$$ Квадрат косинуса: $$\cos^2\alpha=\frac{1+\cos 2\alpha} 2$$
Преобразование выражений вида a sin φ + b sin φ
Сумму синуса и косинуса одного угла, взятых с произвольными коэффициентами a, b, всегда можно представить в виде синуса с некоторым коэффициентом: $$ a \sin \phi + b \sin \phi = A \sin (\phi + \psi), $$ где $$ A = \sqrt{a^2 + b^2}, $$ а \(\psi\) находится из условий $$ \cos \psi = a / A, \\ \sin \psi = b / A, $$ при A = 0, \(\psi\) - любое число.
Для определённости здесь считаем, что A является положительным (точнее, неотрицательным числом), хотя подобное преобразование возможно и для коэффициента \(A = - \sqrt{a^2 + b^2}\). Используемый выбор, когда \(A \ge 0\), более естественен для физических приложений этого преобразования. Например, если рассматривается сложение гармонических колебаний, то A будет амплитудой результирующего колебания, а амплитуду чаще выражают неотрицательными значениями.
Два условия для нахождения \(\psi\) избыточны, если нам известен квадрант, в который попадает угол \(\psi\). Квадрант мы определяем по сочетанию знаков у коэффициентов a, b (которые определяют знак косинуса и синуса этого угла). Например, если оба коэффициента положительны, то угол находится в первом квадранте (где и синус, и косинус угла положительны); если a < 0, b > 0, то это угол из второго квадранта (где косинус отрицателен, а синус положителен) и т.д. Определив квадрант, берём любое одно из двух условий и, рассматривая его как уравнение, находим решение, попадающее в нужный квадрант. После чего все величины в правой части преобразования будут найдены.
Данное преобразование обычно используется не в виде формулы, а получается как результат решения задачи. Допустим, имеем выражение $$ a \sin x + b \cos x, $$ причём коэффициенты a, b не равны одновременно нулю. "Выносим за скобки" множитель \(\sqrt{a^2 + b^2}\) $$ a \sin x + b \cos x = \sqrt{a^2 + b^2} \left( \frac a {\sqrt{a^2 + b^2}} \sin x + \frac b {\sqrt{a^2 + b^2}} \cos x \right). $$ Относительно коэффициентов при sin x, cos x в правой части этого выражения можно утверждать, что сумма их квадратов равна 1. Это означает, что если рассматривать эти числа как координаты некоторой точки, то эта точка находится на единичной окружности, а значит, по определению тригонометрических функций, координаты точки являются соответственно косинусом и синусом некоторого угла (образованного осью Ox и лучом, проходящим через O и эту точку). Обозначим этот угол как \(\psi\), тогда можем записать $$ \cos \psi = \frac a {\sqrt{a^2 + b^2}}, \\ \sin \psi = \frac b {\sqrt{a^2 + b^2}} $$ и, подставляя в предыдущее выражение, получаем $$ a \sin x + b \cos x = \sqrt{a^2 + b^2} ( \cos \psi \sin x + \sin \psi \cos x) = \sqrt{a^2 + b^2} \sin(x + \psi), $$ т.е. преобразовали исходное выражение к требуемой форме.
Конкретный числовой пример: $$ \sqrt 3 \sin x + \cos x = 2 \left( \frac {\sqrt 3} 2 \sin x + \frac 1 2 \cos x \right) = \\ = 2 \left(\cos \frac {\pi} 6 \sin x + \sin \frac {\pi} 6 \cos x \right) = 2 \sin \left( x + \frac {\pi} 6 \right). $$
Сумма синусов (косинусов) от членов арифметической прогрессии.
Сумма синусов от первых n членов арифметической прогрессии вида \( 0, \alpha, 2\alpha, 3\alpha, \ldots \) $$ \sum_{i=0}^{n-1}\sin i\alpha=0+\sin\alpha+\sin 2\alpha+\ldots+\sin(n-1)\alpha= \begin{cases} \frac{\sin\frac{n\alpha}2 \sin\frac{(n-1)\alpha}2} {\sin\frac\alpha 2}, \, если \alpha\neq 2\pi k, k\in Z;\\ 0, \, если \alpha=2\pi k, k\in Z. \end{cases} $$ Сумма косинусов от аналогичной последовательности чисел: $$ \sum_{i=0}^{n-1}\cos i\alpha=1+\cos\alpha+\cos 2\alpha+\ldots+\cos(n-1)\alpha= \begin{cases} \frac 1 2+\frac{\sin\frac{(2n-1)\alpha}2} {2\sin\frac\alpha 2}, \alpha\neq 2\pi k, k\in Z;\\ n, \, если \alpha=2\pi k, k\in Z. \end{cases} $$ Для краткости введём обозначения: $$ Ss_n(\alpha)=\sum_{i=0}^{n-1}\sin i\alpha,\\ Sc_n(\alpha)=\sum_{i=0}^{n-1}\cos i\alpha, $$ тогда для произвольной арифметической прогрессии: \( \phi, \alpha+\phi, 2\alpha+\phi, 3\alpha+\phi, \ldots \), сумма синусов (косинусов) от превых n членов этой прогрессии будет выражаться следующим образом: $$ \sum_{i=0}^{n-1}\sin(i\alpha+\phi)=Sc_n(\alpha)\sin\phi+Ss_n\cos\phi,\\ \sum_{i=0}^{n-1}\cos(i\alpha+\phi)=Sc_n(\alpha)\cos\phi-Ss_n\sin\phi. $$
Довольно интересен тот частный случай, когда \( \alpha=2\pi m/n \) (здесь m - целое число) или, иначе говоря, когда \( n\alpha \) образует какой либо период функции sin или cos (не обязательно минимальный положительный). Тогда $$ Ss_n\left(\frac{2\pi m}n\right)=0\,\text{(всегда)},\\ Sc_n\left(\frac{2\pi m}n\right)= \begin{cases} 0, \text{если }\sin\frac{\pi m}n\neq 0,\\ n, \text{если }\sin\frac{\pi m}n=0. \end{cases} $$
$$ \sum_{i=0}^{n-1}\sin\left(\frac{2\pi m}n i+\phi\right)= \begin{cases} 0, \text{если }\sin\frac{\pi m}n\neq 0,\\ n\sin\phi, \text{если }\sin\frac{\pi m}n=0, \end{cases}\\ \sum_{i=0}^{n-1}\cos\left(\frac{2\pi m}n i+\phi\right)= \begin{cases} 0, \text{если }\sin\frac{\pi m}n\neq 0,\\ n\cos\phi, \text{если }\sin\frac{\pi m}n=0. \end{cases} $$