Сравнение характеристик однофазных умножителей разных типов
В данной статье мы приведём формулы для расчёта выходных характеристик некоторых типов однофазных умножителей напряжения; используя эти формулы, сопоставим свойства умножителей разных типов и выявим возможные области их применения.
Будем рассматривать устройства, относящиеся к типам, которые мы условно обозначили как A, B и Z ("Типы однофазных умножителей напряжения"). Примеры умножителей указанных типов, иллюстрирующие характерные особенности их структуры, приведены соответственно на рис. %img:x8a, рис. %img:x8b, рис. %img:x8z.
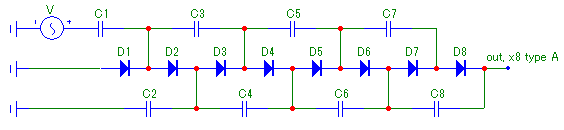
Рис. %img:x8a
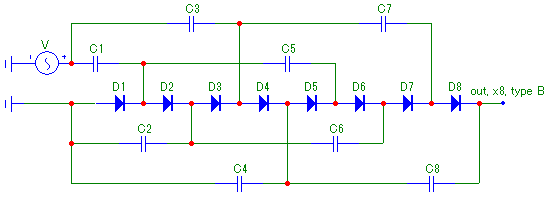
Рис. %img:x8b

Рис. %img:x8z
Для сравнения разных типов умножителей между собой, а также для расчёта параметров элементов конкретного устройства нам потребуются формулы для расчёта выходных характеристик. Устройства типа A уже рассматривались ранее, теперь дополнительно приведём сведения для устройств типа B и Z.
Прежде немного об используемых соглашениях и обозначениях. Будем считать, что рассматриваемые умножители построены из идеальных элементов, коэффициент умножения обозначим через m. Умножитель питается от источника синусоидального напряжения с амплитудой Ua и частотой F. Все конденсаторы имеют одинаковую ёмкость C. При наличии нагрузки, считаем, что она потребляет постоянный ток IL.
Основные обозначения
| m |
коэффициент умножения; |
| Ua |
амплитуда питающего умножитель источника синусоидального напряжения; |
| F |
частота колебаний питающего источника; |
| C |
ёмкость каждого из конденсаторов умножителя; |
| IL |
ток, потребляемый нагрузкой; |
| D=\(|\Delta U_{out}|\) |
величина падения напряжения на выходе умножителя под нагрузкой; |
| h |
размах пульсаций выходного напряжения; |
| Uout_nl=m*Ua |
напряжение на выходе умножителя в установившемся режиме без нагрузки (nl: no-load выходное напряжение); |
| Uout |
напряжение на выходе умножителя в установившемся режиме, при наличии нагрузки Uout<Uout_nl. |
Нам нужно определить напряжение на выходе, Uout. На холостом ходу в установившемся режиме выходное напряжение постоянно и равно Uout_nl=m*Ua. При наличии нагрузки выходное напряжение уменьшается и становится пульсирующим, оно может быть описано некоторой функций времени uout(t), которая является периодической с периодом, равным периоду питающего умножитель напряжения. Однако, обычно на практике такое детализированное описание оказывается излишним. Вполне достаточно указать две величины, одна из которых будет характеризовать постоянную составляющую напряжения на выходе, а другая - уровень пульсаций.
Теперь очень важный момент. В качестве значения - характеристики постоянной составляющей Uout мы будем использовать здесь не саму постоянную составляющую непосредственно, а связанную величину - максимальное, пиковое значение, которого достигают мгновенные значения выходного напряжения (иначе говоря, максимальное значение функции uout(t) за период). Это связано с тем, что именно при таком определении, величина Uout с высокой степенью точности оказывается линейно зависящей от тока нагрузки и может быть вычислена по простым формулам. Если необходимо вычислить постоянную составляющую, то её можно оценить как \(U_{out0}=U_{out}-h/2\), где h - размах пульсаций. В реальных устройствах стремятся добиться малых значений h, так что значение Uout оказывается близким к постоянной составляющей.
Зачастую бывает удобно рассматривать не само выходное напряжение Uout, а его изменение под нагрузкой: \(\Delta U_{out}=U_{out}-mU_a, \Delta U_{out}<0\), либо противоположную ему положительную величину - падение напряжения под нагрузкой \(D=-\Delta U_{out}=mU_a-U_{out}, D>0\).

Рис. %img:load_dg
Размах пульсаций h - величина, равная разности между максимальным и минимальным мгновенным значением выходного напряжения за период. Величину h можно считать примерно пропорциональной току только при малых токах нагрузки. Малыми здесь считаются такие токи, при которых время пребывания диодов в открытом состоянии за период оказывается малым по сравнению с периодом колебаний источника, т.е. когда процессы передачи зарядов между конденсаторами происходят очень быстро. С увеличением тока нагрузки, сопровождающимся увеличением длительности процессов переключения, точность линейного приближения для h падает. Однако, как правило, для практически значимых случаев она оказывается достаточной и, здесь мы будем рассматривать именно линейное приближение (подробнее об этом вопросе смотрите в документе "Умножитель напряжения под нагрузкой. Детализированный анализ").
Для наглядности форма выходного напряжения и некоторые его параметры изображены на рис. %img:load_dg (зелёная линия - уровень холостого хода m*Ua, синяя линия - выходное напряжение как функция времени uout(t), красная линия - график питающего напряжения с амплитудой Ua и периодом T=1/F). Отмечены уровни максимального и минимального значений выходного напряжения Uout, U**out=Uout-h. На рисунке также показано, каким образом отсчитываются величины падения напряжения под нагрузкой D и размаха пульсаций h.
По графику можно проследить процессы в умножителе. Быстрые изменения функции uout(t) соответствуют тем промежуткам времени, когда открываются диоды умножителя, обеспечивая передачу заряда между конденсаторами. Медленные изменения, делающие наклонными вершины и основания импульсов, происходят в результате разряда сглаживающих конденсаторов током нагрузки при закрытых диодах умножителя. Максимальное мгновенное значение напряжения на выходе достигается, когда напряжение питающего источника V=+Ua и сглаживающие конденсаторы (по крайней мере, в устройствах типов A, B, Z) максимально заряжены (кстати, разделительные конденсаторы в этот момент максимально разряжены). Когда V=-Ua, мгновенное напряжение на выходе достигает минимального значения (заряд на сглаживающих конденсаторах в этот момент минимальный, а на разделительных - максимальный). Форма напряжения на отдельных конденсаторах также имеет вид импульсов. На сглаживающих конденсаторах она аналогична форме выходного напряжения. На разделительных импульсы инверсны по отношению к импульсам на сглаживающих, а кроме того, вершины и основания являются горизонтальными, так как эти конденсаторы при закрытых диодах не разряжаются током нагрузки.
Таблица %tbl:formulas
| Тип |
Падение напряжения, D |
Размах пульсаций*, h |
Максимальная запасённая энергия, W |
A0
(m=2, 4, 6, ...) |
\(d\left(\frac{m^3}6+\frac{m^2}8+\frac m{12}\right)\) |
\(d\left(\frac{m^2}4+\frac m 2\right)\) |
\(W_0(4m-3)\) |
A1
(m=1, 3, 5, ...) |
\(d\left(\frac{m^3}6+\frac{m^2}8-\frac m 6-\frac 1 8\right)\) |
\(d\left(\frac{m^2}4+m+\frac 3 4\right)\) |
B0
(m=4, 8, 12, ...) |
\(d\left(\frac{m^3}{24}+\frac{5m^2}{32}+\frac{5m}{24}\right)\) |
\(d\left(\frac{m^2}{16}+\frac m 4\right)\) |
\(W_0(16m-34),\\ \text{если }m\ge3, \\
W_0(4m-3),\\ \text{если }m<3\) |
B1
(m=1, 5, 9, 13, ...) |
\(d\left(\frac{m^3}{24}+\frac{5m^2}{32}+\frac m{48}-\frac 7{32}\right)\) |
\(d\left(\frac{m^2}{16}+\frac{5m}8+\frac{21}{16}\right)\) |
B2
(m=2, 6, 10, 14, ...) |
\(d\left(\frac{m^3}{24}+\frac{5m^2}{32}+\frac m 3+\frac 3 8\right)\) |
\(d\left(\frac{m^2}{16}+\frac m 2+\frac 3 4\right)\) |
B3
(m=3, 7, 11, 15, ...) |
\(d\left(\frac{m^3}{24}+\frac{5m^2}{32}+\frac{19m}{48}+\frac 9{32}\right)\) |
\(d\left(\frac{m^2}{16}+\frac{3m}8+\frac 5{16}\right)\) |
Z
|
\(d(2m-2)\) |
\(2d\) |
\(W_0\left(\frac{n^3}3+\frac{n^2}2+\frac n 6\right)\) |
* Формулы для размаха пульсаций приведены в линейном приближении и при больших токах нагрузки могут давать ощутимую погрешность.
$$d=\frac{I_L}{2FC},\\
W_0=\frac{CU_a^2}2.$$
В таблице под коэффициентом d, который также обозначался ранее в других документах как \(\Delta U\) (не путать с \(\Delta U_{out}\)), подразумевается величина \(d=\Delta U=\frac{I_L}{2FC}\). Физический смысл её состоит в том, что она показывает, насколько упадёт напряжение конденсатора с ёмкостью C при разряде его током нагрузки IL в течение времени \(\tau\), равного половине периода (т.е. равного длительности одного полуцикла работы умножителя): \(\tau=T/2=1/(2F)\).
Как видим, тип A требует разделения на два подтипа: с чётным (A0) и нечётным (A1) коэффициентом умножения (иначе говоря, дающие в остатке при делении m на 2 значения 0 или 1). A0 и A1 имеют несколько отличающиеся выражения для вычисления параметров D и h, однако характер зависимостей у них одинаков и с ростом m относительное расхождение между выражениями для подтипов стремится к 0.
Тип B имеет уже 4 подтипа B0, B1, B2, B3 (в зависимости от значения, получаемого в остатке при делении m на 4). Здесь также наблюдается небольшое различие в выражениях, но одинаковый характер зависимостей со стремящимися к 0 относительными расхождениями между ними при возрастании m.
Наиболее однородным оказывается тип Z, занимающий одну строку таблицы. Все устройства типа Z описываются общими выражениями, независимо от значения m.
Кстати, при малых m происходит вырождение устройств других типов в тип Z. Так, устройства типа B становятся неотличимыми от Z при \(m\le 4\). Устройства типа A неотличимы от Z при \(m\le 2\). При этом, формально, формулы для типов A и B остаются применимыми и при малых m, это можно проверить по таблице непосредственной подстановкой значений - для эквивалентных устройств разные формулы будут давать одинаковые значения.
Уточнённый расчёт h для умножителей типа A (с чётным коэффициентом умножения) приводится в документе "Умножитель напряжения под нагрузкой. Детализированный анализ". Там показано, что размах пульсаций
$$
h=d\frac{m^2}4+\gamma \theta \frac m 2, \text{ где} \\
\gamma=\frac{I_L}C,
$$
а \(\theta\) - так называемая длительность пассивной фазы полутакта, время от конца одного перезаряда конденсаторов до начала следующего, в течение которого все диоды умножителя закрыты. Может быть найдена из уравнения
$$
-U_a\left(\cos\frac{2\pi\theta}T+1\right)+\gamma\theta\left(-\frac{3m}4+\frac 1 2\right)+\gamma \frac T 2 \left(\frac{3m}4-\frac 1 2+\frac{m^2}2\right)=0,
$$
которое решается только численными методами. Приблизительно может быть вычислена как
$$
\theta \approx \frac 1 {\omega} \arccos\left( \frac{d}{U_a}\frac{m^2}2-1 \right)
$$
или ещё более приблизительно
$$
\theta \approx \frac T 2 - \frac m{\omega} \sqrt{\frac{d}{U_a}}.
$$
Уточнённое значение h оказывается несколько меньше, чем полученное в линейном приближении. Это можно объяснить тем, что в действительности время перезаряда конденсаторов отлично от нуля, и в это время некоторые из диодов открыты, обеспечивая питание нагрузки не только за счёт разряда сглаживающих конденсаторов, но и отчасти за счёт разделительных.
| Результат для исходных данных: |
m = ...; C = ...;
Ua = ...; F = ...;
IL = ...
|
| m*Ua = ... |
| d = ... |
| |
| |
Тип A |
Тип B |
Тип Z |
| D = d * |
... |
... |
... |
| D = |
... |
... |
... |
| h = d * |
... |
... |
... |
| h = |
... |
... |
... |
Примечание. При расчётах не контролируется область применимости формул по токам нагрузки. Поэтому возможно получение результата для D или h, превышающего выходное напряжение холостого хода. Это означает, что умножитель уже перегружен и не будет нормально работать в таком режиме.
Если сравнивать умножители типов A, B, Z с одинаковым коэффициентом умножения и одинаковой ёмкостью конденсаторов, то, как видим из таблицы, безусловным победителем является умножитель типа Z. Он имеет минимальный размах пульсаций h, который к тому же не зависит от коэффициента умножения! Выражения для размаха пульсаций умножителей типов A, B имеют вид полиномов второй степени относительно коэффициента умножения m, соответственно, с увеличением m, амплитуда пульсаций будет довольно сильно возрастать. Но при этом умножители типа B, оказываются лучше по сравнению с типом A. С ростом m отношение для h у типов A, B (hB/hA) стремится к 1/4 - тип B в пределе имеет четырёхкратное превосходство над A по малости размаха пульсаций.
Что касается падения напряжения под нагрузкой, тут также выигрышным оказывается вариант Z, показывая меньшие значения величины D и более медленный рост с увеличением m. Имеет место всего лишь линейная зависимость D от m, в то время как зависимость для типов A, B описывается полиномами третьей степени! Если сравнивать между собой типы A и B, то лучшие показатели видим у умножителей типа B, в пределе, с ростом m, падение напряжения у них оказываются в 4 раза меньше, чем у аналогичных умножителей типа A.
Однако, сравнивать разные типы только с учётом выходных характеристик было бы не вполне корректно. Как мы знаем, умножители разных типов отличаются друг от друга напряжениями на конденсаторах, а значит, они требуют использования конденсаторов с разными номинальными напряжениями. В то же время номинальное напряжение - крайне важный параметр, не в меньшей мере, чем ёмкость, влияющий на
массогабаритные показатели и стоимость, как отдельного конденсатора, так и всего устройства в целом.
Можно легко показать, что объём диэлектрика в конденсаторе пропорционален его ёмкости и пропорционален квадрату номинального напряжения. Если технология изготовления конденсаторов данного типа достаточно совершенна и можно считать, что объём и масса материала обкладок много меньше, чем диэлектрика, то объём и массу конденсатора в целом можно считать пропорциональными произведению \(CU^2_{nom}\). С учётом того, что максимальная энергия, которая может быть накоплена в конденсаторе без выхода за предельные режимы эксплуатации, выражается как \(W_{max}=CU^2_{nom}/2\), то данную величину также можно рассматривать как меру объёма (или массы) конденсатора.
Именно поэтому в таблице %tbl:formulas приведена колонка с формулами для вычисления энергии, которая накапливается конденсаторами умножителя в установившемся режиме на холостом ходу. Эта величина позволяет судить о минимально достижимом суммарном объёме (массе) всех конденсаторов умножителя. Для того чтобы достичь этого минимально возможного объёма, каждый конденсатор в схеме должен быть подобран с номинальным напряжением, равным напряжению на нём при работе в умножителе (в режиме холостого хода). Если номинальное напряжение выбирается больше реального, например, из соображений надёжности или из-за отсутствия конденсатора с требуемым параметром, получаем рост
массогабаритных показателей устройства без улучшения параметров D и h из-за недоиспользования конденсаторов по напряжению.
Наибольший интерес для нас представляет даже не само значение энергии, а соотношение значений для устройств разных типов с учётом выходных параметров устройств. Такое сопоставление даёт возможность судить об эффективности использования единицы объёма (массы) конденсаторов для получения наилучших характеристик устройства.
Сравним теперь умножители разных типов (но с одинаковым коэффициентом умножения m), при условии, что они имеют одинаковый минимально достижимый суммарный объём конденсаторов (что эквивалентно, как мы установили, равенству энергии конденсаторов на холостом ходу у этих умножителей). В качестве базовой, единичной энергии, будем считать энергию конденсаторов умножителя типа A:
$$
W_A=W_0(4m-3) \text{ или } \\
W_A=\frac {CU_a^2}2 (4m-3).
$$
Будем подбирать ёмкость конденсаторов Cx другого рассматриваемого умножителя так, чтобы общая энергия конденсаторов на холостом ходу у данных умножителей совпала (тогда совпадут и минимальные суммарные объёмы конденсаторов).
$$
\frac{C_xU_a^2}2 K=\frac {CU_a^2}2 (4m-3),
$$
здесь K - коэффициент, зависящий от типа умножителя и коэффициента умножения, такой, что \(W=W_0K\), значения K смотрите в таблице %tbl:formulas; (4m-3) это значение коэффициента для типа A. Тогда
$$
C_x=\frac{C(4m-3)}K.
$$
Если конденсаторы второго умножителя будут иметь указанную ёмкость Cx, суммарная энергия конденсаторов и суммарный минимально достижимый объём получатся такими же, как у умножителя типа A с конденсаторами ёмкостью C.
Пример. На рис. %img:eqv изображены схемы двух умножителей напряжения на 3, один - типа A, второй - типа Z. Если ёмкость конденсаторов в первом равна C, то во втором она должна быть Cx=C*9/14, чтобы получить одинаковые минимально достижимые суммарные объёмы конденсаторов в этих устройствах. Если C=1 мкФ, то Cx примерно составит 0.64 мкФ.
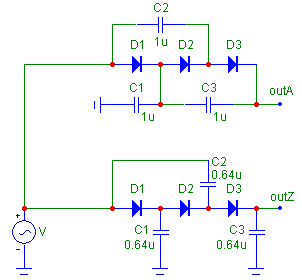
Рис. %img:eqv
Выражение для Cx мы можем подставить в формулу для вычисления значения d, которому пропорциональны падение выходного напряжения под нагрузкой D и размах пульсаций h и получить выражения для нормированных характеристик Dnorm и hnorm. Так, для нормированных выходных характеристик умножителей типов B и Z имеем
$$
D_{Bnorm}=D_B\frac {16m-34}{4m-3}, \\
D_{Znorm}=D_Z\frac {\frac{m^3}3+\frac{m^2}2+\frac m 6}{4m-3},
$$
где DB, DZ - падения выходного напряжения под нагрузкой в умножителях B, Z, которое было бы при ёмкости конденсаторов равной C (формулы смотрите в таблице); DBnorm, DZnorm - величины падения напряжения в умножителе с конденсаторами ёмкостью Cx, т.е. с
суммарным объёмом конденсаторов как у умножителя типа A с конденсаторами ёмкости C. Надеюсь, что объяснение не слишком запутанное.
Аналогичными получаются выражения для нормированных величин размаха пульсаций:
$$
h_{Bnorm}=h_B\frac {16m-34}{4m-3}, \\
h_{Znorm}=h_Z\frac {\frac{m^3}3+\frac{m^2}2+\frac m 6}{4m-3}.
$$
Выписывать выражения полностью в общем виде особого смысла нет - они получаются довольно громоздкими и ненаглядными. Поступим иначе: рассмотрим поведение нормированных характеристик при \(m\to\infty\), а затем, вычислим для нескольких небольших значений m.
Можно легко показать, что
$$
\lim\limits_{m\to\infty}\frac{D_{Bnorm}}{D_A}=1, \\
\lim\limits_{m\to\infty}\frac{D_{Znorm}}{D_A}=1,
$$
что говорит нам об одинаковой эффективности всех рассматриваемых типов с точки зрения падения напряжения под нагрузкой при больших коэффициентах умножения m. Иначе говоря, от умножителей одинакового объёма можно ожидать одинаковых значений параметра D, независимо от типов этих умножителей.
Вычисляя аналогичные пределы для размаха пульсаций, получим
$$
\lim\limits_{m\to\infty}\frac{h_{Bnorm}}{h_A}=1, \\
\lim\limits_{m\to\infty}\frac{h_{Znorm}}{h_A}=2/3,
$$
т.е., умножитель типа B имеет такую же эффективность, как и A при больших m. Умножитель Z лучше A по размаху пульсаций, у типа Z они оказались в 1.5 раза меньше, что существенно.
Посмотрим теперь на показатели разных типов умножителей при небольших m, что представляет особый интерес, так как именно такие умножители используются чаще всего. В таблице приведены коэффициенты эффективности - отношения соответствующих величин (выходных характеристик) у умножителей данного типа (B или Z) и умножителя типа A с таким же минимально достижимым суммарным объёмом конденсаторов (или такой же суммарной энергией на холостом ходу, всё равно). Ток нагрузки, естественно, предполагается одинаковым. Чем меньше величина в таблице, тем меньше у данного умножителя падение напряжения под нагрузкой или меньше размах пульсаций по сравнению с умножителем типа A с такими же массогабаритными характеристиками. А значит, тем эффективнее данная схема, тем лучше её удельные показатели (показатели в расчёте на единицу объёма).
| m |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| \(\frac{D_{Bnorm}}{D_A}\) |
1 |
1.244 |
1.065 |
1.059 |
1.224 |
1.258 |
1.137 |
1.103 |
1.154 |
1.164 |
1.109 |
1.088 |
1.113 |
1.119 |
| \(\frac{D_{Znorm}}{D_A}\) |
1 |
1.244 |
1.065 |
1.125 |
1.057 |
1.084 |
1.048 |
1.063 |
1.041 |
1.050 |
1.035 |
1.042 |
1.031 |
1.036 |
| \(\frac{h_{Bnorm}}{h_A}\) |
1 |
0.519 |
0.769 |
1.353 |
1.476 |
0.936 |
0.972 |
1.333 |
1.362 |
0.990 |
1.003 |
1.268 |
1.280 |
1.004 |
| \(\frac{h_{Znorm}}{h_A}\) |
1 |
0.519 |
0.769 |
0.539 |
0.722 |
0.56 |
0.703 |
0.576 |
0.694 |
0.588 |
0.688 |
0.597 |
0.684 |
0.604 |
В колонке для m=2 все значения равны 1, это следствие того, что существует единственная схема однофазного однополярного удвоителя напряжения и какое-либо деление на типы для удвоителей невозможно. Варианты, позволяющие разделять схемы на типы, появляются при m>2.
Отметим также, что при m меньших 5, схема типа B вырождается в схему типа Z, поэтому в первых колонках (m=2..4) можем видеть одинаковые значения соответствующих коэффициентов. При больших значениях m, как и следовало ожидать, коэффициенты падения напряжения приближаются к 1, т.е. все три схемы оказываются в одинаковой степени эффективными по параметру D. Коэффициент пульсаций при увеличении m стремится к 1 для схемы типа B. Для схем типа Z с увеличением m наблюдается изменение коэффициента пульсации вблизи значений 0.6..., что согласуется с полученным нами предельным значением 2/3.
Изменения величин с ростом m носят немонотонный характер, что, прежде всего, связано с зависимостью характеристик умножителей типа A, взятых за эталон, от чётности коэффициента умножения.
По таблице можно легко определить удачные и неудачные варианты реализации умножителей (при условии минимального объёма). Например, интересный вариант - умножитель на 3 типа Z, он хотя и уступает умножителю типа A по падению напряжения (примерно на 24%), но зато имеет почти в два раза меньший коэффициент пульсаций при том же объёме конденсаторов! А вот умножитель типа B с коэффициентом 6 уступает умножителю типа A по всем параметрам, и весьма ощутимо: имеет большее падение напряжение под нагрузкой (примерно на 22%) и большую амплитуду пульсаций (почти в 1.5 раза).
Ещё раз обратим внимание, что при вычислении коэффициентов эффективности здесь сравниваются два умножителя не с одинаковыми ёмкостями конденсаторов, а с разными, подобранными так, что суммарный объём конденсаторов каждого из умножителей оказывается одинаковым.
-
A тип.
Устройства типа A являются оптимальными для использования в высоковольтных преобразователях напряжения. Также этот тип может быть выбран, если нет уверенности в том, на чём остановиться или нет желания глубоко погружаться в изучение данной проблемы. Тип A является даже если и не оптимальным, то достаточно хорошим решением для большинства случаев.
-
Z тип.
Устройства типа Z показывают наилучшие характеристики в низковольтных устройствах.
-
B тип.
Устройства типа B (и аналогичные им) могут оказаться наиболее предпочтительными в некоторых промежуточных ситуациях, когда напряжения уже слишком высоки для типа Z, но ещё низки для того, чтобы в умножителях типа A конденсаторы достаточно полно использовались по напряжению.
Поясним предложенные рекомендации.
Отличительная особенность умножителей типа A, определяющая их основную область применения - минимальное напряжение на конденсаторах (2*Ua, а на первом Ua) по сравнению со всеми прочими типами. Данное свойство оказывается очень ценным в случае высоковольтных устройств, где с ростом рабочих напряжений конденсаторов резко возрастает их стоимость, а номенклатура доступных элементов неумолимо сокращается.
Теоретически, имея сравнительно низковольтный источник переменного напряжения и низковольтные конденсаторы, можем построить умножитель типа A со сколь угодно высоким напряжением на выходе. В этом состоит принципиальное отличие от типа Z, где напряжение на каждом последующем конденсаторе выше, чем на предыдущем, достигая на последнем полного выходного напряжения умножителя.
Приятным дополнением к основной особенности типа A являются хорошие выходные характеристики. В зависимости от коэффициента умножения, устройства этого типа могут немного превосходить своих конкурентов по некоторым показателям, в некоторых случаях могут немного, но не критически уступать. Более подробно характеристики, в том числе и удельные, сравниваются в предыдущем пункте.
В области низких напряжений ситуация кардинально изменяется. Как было указано в предыдущем пункте, по большому счёту удельные характеристики всех типов умножителей отличаются не слишком сильно, как правило, различие между типами не превышает десятка или двух десятков процентов. Но это при условии, что номинальное напряжение каждого конденсатора выбрано близким к его максимальному рабочему (в режиме холостого хода).
Однако, номинальное напряжение конденсатора (максимально допустимое напряжение) - не тот параметр, который мы можем задавать произвольно. Как правило, имеем дело с выбором из весьма ограниченного ряда значений. Допустим, мы выбрали для использования подходящий тип конденсаторов, подобрав его по максимальной рабочей частоте, максимально допустимому уровню переменной составляющей напряжения, динамическим потерям, току утечки и пр. Может оказаться, что даже минимальное напряжение из предлагаемого ряда номинальных значений для этого типа конденсаторов будет не только выше значения 2*Ua, но и даже выше выходного напряжения умножителя.
В описанной ситуации мы в принципе не можем достичь теоретически минимального суммарного объёма конденсаторов устройства из-за того, что вынуждены мириться с недоиспользованием конденсаторов по напряжению.
В подобных случаях задача оптимального выбора сводится к минимизации ёмкости конденсаторов для получения требуемых параметров. Без учёта напряжений. Это означает, что наилучшим вариантом является умножитель типа Z, обеспечивающий минимальные D и h по сравнению с другими типами при одной и той же ёмкости конденсаторов: таблица %tbl:formulas.
Если m*Ua оказывается слишком большим, но, по-прежнему 2*Ua слишком мало для эффективного использования конденсаторов в схеме A типа, то, возможно, оптимальным окажется умножитель B или подобного типа.
Предположим, нам требуется построить умножитель с коэффициентом m минимального объёма, но ещё непонятно, какой тип выбрать. Если тип A однозначно не обеспечивает минимизацию объёма (доступное номинальное напряжение конденсаторов многократно превышает величину 2*Ua), но и тип Z не подходит (m*Ua превышает номинальное напряжение для конденсатора), то поступаем следующим образом.

Рис. %img:tbb1
Начинаем построение с типа Z, рис. %img:tbb1 (на рисунке рядом с каждым конденсатором указано напряжение на нём относительно амплитуды питающего напряжения при работе в режиме холостого хода). Последовательно наращиваем умножитель, добавляя по одному звену. На каком-то шаге напряжение на очередном конденсаторе окажется слишком высоким (рис. %img:tbb2). Это означает, что этот и последующие конденсаторы следует подключать не к общему проводу (сглаживающий) или источнику переменного напряжения (разделительный), а к одному из предыдущих узлов диодной цепи, без переменной или с переменной составляющей потенциала соответственно. Так, если применить этот приём, начиная с пятого конденсатора, обеспечивая на нём и последующих напряжение 4*Ua (в режиме холостого хода), то получим схему типа B (рис. %img:tbb3).

Рис. %img:tbb2

Рис. %img:tbb3
Если начнём с 7-го конденсатора, то получим умножитель, напряжения на конденсаторах которого, начиная с 6-го, будут равны в режиме холостого хода 6*Ua (Рис. %img:tcb1). По аналогии с типом B, можем назвать полученный тип умножителя типом C.

Рис. %img:tcb1
Рассмотренные выше примеры относились к умножителям с чётным коэффициентом, но всё то же самое справедливо и для устройств с нечётным коэффициентом. Так, на рис. %img:tbb_odd изображена схема умножителя на 7 типа B. Здесь имеем одно звено (D6, D7 + конденсаторы при них), включённое по правилам формирования структуры B-типа.

Рис. %img:tbb_odd
Заметим, что если используется подключение конденсаторов между узлами диодной цепи, то напряжения на конденсаторах оказывается равным n*Ua, где n - обязательно чётное число. Действительно, чтобы конденсатор был включён между соответственными узлами (одновременно имеющими или не имеющими переменной составляющей потенциала), мы должны пропустить нечётное количество узлов, следовательно, конденсатор будет "охватывать" чётное количество диодов. Но каждый диод обеспечивает в умножителе прирост напряжения на Ua, так что напряжение на конденсаторе действительно окажется в чётное число раз больше Ua.
Таким образом получаем, что в умножителях напряжение на конденсаторах не превышает:
для типа A: 2*Ua;
для типа B: 4*Ua;
для типа C: 6*Ua;
для типа D: 8*Ua;
...
При этом соответственно первые 2, 4, 6, 8, ... D-C элементов образуют не что иное, как умножитель Z-типа. То есть, все эти умножители начинаются с цепочки из нескольких звеньев Z-умножителя большей или меньшей длины. И чем эта цепочка длиннее, тем эффективнее умножитель при условии неизменности ёмкости используемых конденсаторов - тип B будет эффективнее, чем A, С - эффективнее B и т.д., Z эффективнее их всех. Но, опять же, это - при условии равной ёмкости конденсаторов; при условии равной суммарной энергии конденсаторов, типы становятся сопоставимы по характеристикам.
Что дальше?
Здесь были приведены расчётные формулы для умножителей разных типов, но не приводится их вывод. Для типа A вывод формул был выполнен ранее, для типа B, возможно, вывод будет добавлен позже (материалы имеются, готовятся к публикации). Впрочем, анализировать аналитически каждый отдельный тип умножителей - довольно трудоёмкий путь, особенно с учётом потенциально неограниченного количества возможных типов. Более перспективным представляется построение автоматизированного средства для анализа любого заданного умножителя напряжения, смотрите "Универсальный решатель умножителей".
author: hamper; date: 2019-01-30












